- a)
- Sei
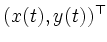 die von der Zeit
die von der Zeit 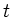 abhängige
Wegfunktion des Hundes. Die Geschwindigkeit ergibt sich aus der
Ableitung der Wegfunktion. Sie setzt sich aus dem zum Ursprung
orientierten Vektor der Länge
abhängige
Wegfunktion des Hundes. Die Geschwindigkeit ergibt sich aus der
Ableitung der Wegfunktion. Sie setzt sich aus dem zum Ursprung
orientierten Vektor der Länge 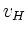 und dem Geschwindigkeitsvektor
des Flusses zusammen:
und dem Geschwindigkeitsvektor
des Flusses zusammen:
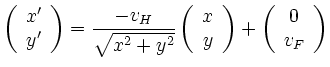 |
(1) |
- b)
- Division der zweiten Komponentengleichung durch
die erste liefert die homogene Differentialgleichung
Die Substitution
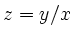 liefert mit
liefert mit  und
und
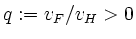 eine separable Differentialgleichung:
Beidseitige Integration und Resubstitution ergibt
Bestimmung von
eine separable Differentialgleichung:
Beidseitige Integration und Resubstitution ergibt
Bestimmung von 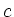 mit Hilfe des Anfangswertes
mit Hilfe des Anfangswertes 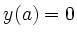 :
Bahnfunktion des Hundes:
:
Bahnfunktion des Hundes:
Damit der Hund die Wurst erreicht, muss gelten
d.h. die Geschwindigkeit des Hundes muss größer als die des Flusses
sein.
- c)
- Erste Komponentengleichung von (1)
ist eine separable Differentialgleichung mit
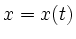 :
Substitution von
:
Substitution von 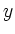 gemäß (2) und beidseitige
Integration liefert:
gemäß (2) und beidseitige
Integration liefert:
Verwende Anfangswert 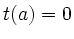 zur Bestimmung der Konstanten
zur Bestimmung der Konstanten 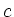 :
Der Hund erreicht sein Ziel bei
:
Der Hund erreicht sein Ziel bei 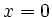 , also zum Zeitpukt
, also zum Zeitpukt  .
.
- d)
- Ein Student möchte ein Studium in einer bestimmten Zeit schaffen,
wobei das Diplom sein Ziel ist. Der Student hat immer den gleichen
Arbeitseifer mit dem er seinem Diplom näher kommt. Leider überlagert sich
sein Arbeitseifer mit seiner natürlichen Faulheit. Dadurch kommt es zu
Verzögerungen und der Student benötigt am Ende etwas mehr Zeit als er
ursprünglich geplant hatte.
(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
| |
automatisch erstellt
am 28.10.2006 |


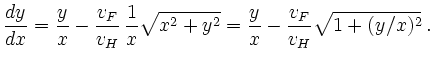
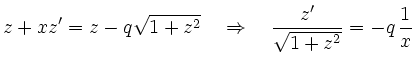
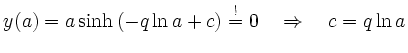
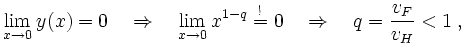


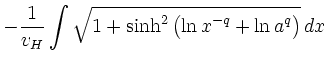
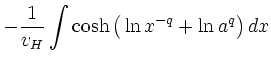
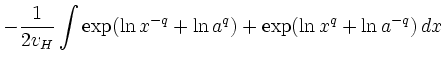
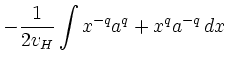
![$\displaystyle -\frac{1}{2v_{H}}\left[\frac{a^{q}x^{1-q}}{1-q}+\frac{a^{-q}x^{q+1}}{q+1}\right]+c$](/inhalt/loesung/loesung837/img29.png)
![$\displaystyle t(a)=-\frac{1}{2v_{H}}\left[\frac{a}{1-q}+\frac{a}{q+1}\right]+c\...
...Rightarrow \quad
c=\frac{a}{v_{H}(1-q^{2})}=\frac{av_{H}}{v_{H}^{2}-v_{F}^{2}}
$](/inhalt/loesung/loesung837/img31.png)