Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 12

Blatt 12, Aufgabe 1

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

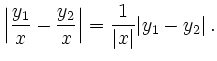
  1. $\displaystyle \left\vert \frac {y_1}x - \frac {y_2} x\right\vert = \frac1{\vert x\vert} \vert y_1-y_2\vert\,. $

    Für alle $ (x_0,y_0)$ mit $ x_0\neq 0$ ist also die Lipschitzbedingung in einer Umgebung erfüllt.

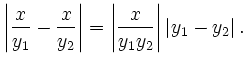
  2. $\displaystyle \left\vert \frac x{y_1} - \frac x{y_2}\right\vert = \left\vert \frac{x}{y_1y_2} \right\vert\vert y_1-y_2\vert\,. $

    Für alle $ (x_0,y_0)$ mit $ y_0\neq 0$ ist also die Lipschitzbedingung in einer Umgebung erfüllt.

  3. $\displaystyle 3\left\vert \sqrt[3]{y_1^2} - \sqrt[3]{y_2^2}\right\vert = 3\left... ...}^2+ \sqrt[3]{y_1^2y_2^2} + \sqrt[3]{y_2^2}^2}\right\vert\vert y_1-y_2\vert\,. $

    Für alle $ (x_0,y_0)$ mit $ y_0\neq 0$ ist also die Lipschitzbedingung in einer Umgebung erfüllt.
(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 28.10.2006