Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 12

Blatt 12, Aufgabe 5

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Zu bestimmen ist die allgemeine reelle Lösung des Differentialgleichungssystems:

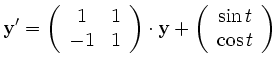
$\displaystyle \textbf{y}'= \left(\begin{array}{cc} 1&1 \\ -1&1 \\ \end{array}... ...t \textbf{y} + \left(\begin{array}{c} \sin t \\ \cos t \\ \end{array}\right) $

Man bestimmt zunächst die allgemeine homogene Lösung, also die Lösung des DGL-Systems:

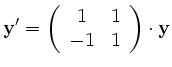
$\displaystyle \textbf{y}'= \left(\begin{array}{cc} 1&1 \\ -1&1 \\ \end{array}\right)\cdot \textbf{y} $

Dazu berechnet man die Eigenwerte und zugehörigen Eigenvektoren der Matrix:

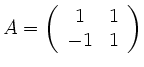
$\displaystyle A=\left(\begin{array}{cc} 1&1 \\ -1&1 \\ \end{array}\right) $


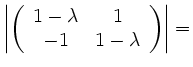$\displaystyle \det(A-\lambda \cdot E)$ $\displaystyle =$ $\displaystyle \left\vert \left( \begin{array}{cc} 1-\lambda & 1 \\ -1 & 1-\lambda \\ \end{array}\right) \right\vert=$  
       
  $\displaystyle =$ $\displaystyle {}(1-\lambda)^2 +1$  
  $\displaystyle =$ $\displaystyle {}\lambda^2-2\lambda+2=0$  

Die Matrix A besitzt also nur die komplexen EWe:

$ \lambda_{1}= 1-i$,          $ \lambda_{2}= 1+i$,

Man bestimmt nun die EVen entsprechend dem Verfahren in 13.2) zu:

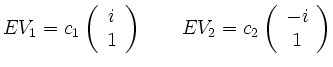
$\displaystyle EV_{1}=c_1\left(\begin{array}{c} i \\ 1 \\ \end{array}\right) \qquad EV_{2}=c_2 \left(\begin{array}{c} -i \\ 1 \\ \end{array}\right) $

Damit hat man als allgemeine komplexe homogene Lösung:

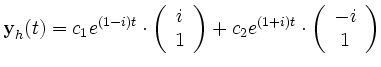
$\displaystyle \textbf{y}_h(t)=c_1e^{(1-i)t}\cdot \left(\begin{array}{c} i \\ 1... ...ght)+c_2e^{(1+i)t}\cdot \left(\begin{array}{c} -i \\ 1 \\ \end{array}\right) $

Da bei einer komplexen Lösung und einer Matrix A mit ausschließlich reellen Koeffizienten immer auch Real- und Imaginärteil für sich Lösungen des DGL-Systems sind, kann hier als allgemeine, homogene Fundamentalmatrix angegeben werden:

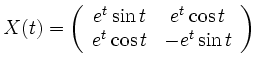
$\displaystyle X(t)=\left(\begin{array}{cc} e^t\sin t&e^t\cos t \\ e^t\cos t&-e^t\sin t\\ \end{array}\right) $

Eine partikuläre Lösung ergibt sich durch:

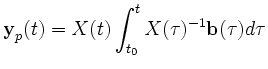
$\displaystyle \textbf{y}_p(t) = X(t)\int_{t_0}^tX(\tau)^{-1}\textbf{b}(\tau)d\tau $

mit

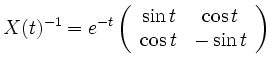
$\displaystyle X(t)^{-1}= e^{-t}\left(\begin{array}{cc} \sin t& \cos t \\ \cos t&-\sin t \\ \end{array}\right) $

zu

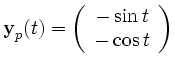
$\displaystyle \textbf{y}_p(t)= \left(\begin{array}{c} -\sin t \\ -\cos t\\ \end{array}\right) $

Damit lautet die allgemeine reelle Lösung des vorliegenden DGL-Systems:

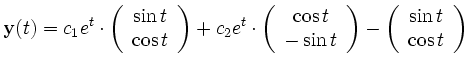
$\displaystyle \textbf{y}(t)=c_1e^t \cdot \left(\begin{array}{c} \sin t \\ \cos... ...array}\right)- \left(\begin{array}{c} \sin t \\ \cos t \\ \end{array}\right) $

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 28.10.2006