Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik-Lösungen-Übungsblatt 4-Blatt 4, Aufgabe 2

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 4
	Blatt 4, Aufgabe 2

a)

Mit der Substitution

$\displaystyle u=e^x \,,\quad du=e^x\,dx$

erhält man

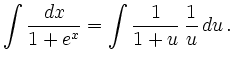
$\displaystyle \int \frac{dx}{1+e^x} = \int \frac{1}{1+u}\, \frac{1}{u}\, du \,.$

Mit Hilfe der Partialbruchzerlegung

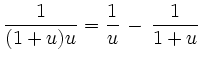
$\displaystyle \frac{1}{(1+u)u} = \frac{1}{u}\,-\, \frac{1}{1+u}$

ergibt sich die Stammfunktion

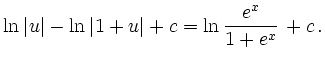
$\displaystyle \ln \vert u\vert - \ln \vert 1+u\vert +c = \ln \frac{e^x}{1+e^x}\,+ c\,.$

b)

Mit der Substitution

$\displaystyle u=\sqrt{x}\,,\quad du = \frac{1}{2\sqrt{x}}\, dx\,,\quad x\in[0,\pi^2] \Leftrightarrow u \in [0,\pi]$

erhält man

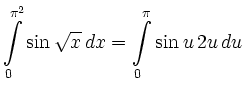
$\displaystyle \int\limits_0^{\pi^2} \sin \sqrt{x}\, dx = \int\limits_0^\pi \sin u \, 2u\, du$

und mit partieller Integration den Wert

$\displaystyle \left[-\cos u\, (2u) \right]_0^\pi -\int\limits_0^\pi -\cos u\, 2\, du = -(-1)(2\pi)+0+\left[2 \sin u\right]_0^\pi = 2\pi\,.$

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)

automatisch erstellt am 28.10.2006