Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Mathematik II für Informatik und Softwaretechnik - Lösungen - Übungsblatt 7

Blatt 7, Aufgabe 1

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Bei Messungen in den Zeitpunkten 1h, 2h, 3h, 4h und 5h erhält man folgende Meßreihe: 0.3, 1.0, 1.9, 3.1 und 4.7.
Beschreiben Sie diese Meßreihe durch eine Ausgleichsgerade nach der Methode der kleinsten Fehlerquadrate.



$ x_{i}$ $ y_{i}$ $ x_{i}^2$ $ x_{i}y_{i}$ $ \varphi(x_{i}) ~ \vert ~ y=1.07+1.09x_{i}$ Abweichung Messwerte
1 0.3 1 0.3 0.02 -0.28
2 1.0 4 2.0 1.11 0.11
3 1.9 9 5.7 2.20 0.30
4 3.1 16 12.4 3.29 0.19
5 4.7 25 23.5 4.38 -0.32
15 11.0 55 43.9   0.00




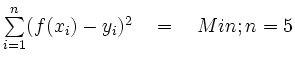
Forderung:          $ \sum \limits_{i=1}^{n} (f(x_{i})-y_{i})^2 \quad = \quad Min \hfill ;n=5$


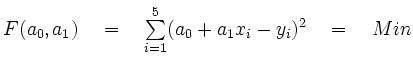
$ F(a_{0},a_{1}) \quad = \quad \sum \limits_{i=1}^{5} (a_{0}+a_{1}x_{i}-y_{i})^2 \quad = \quad Min$




1. notwendige Bedingung: 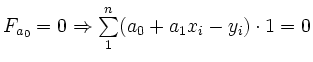     $ F_{a_{0}} = 0 \hfill \Rightarrow \sum \limits_{1}^{n} (a_{0}+a_{1}x_{i}-y_{i})\cdot 1 = 0$     (1)


2. notwendige Bedingung: 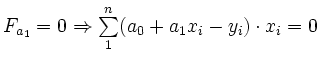     $ F_{a_{1}} = 0 \hfill \Rightarrow \sum \limits_{1}^{n} (a_{0}+a_{1}x_{i}-y_{i}) \cdot x_{i} = 0$     (2)


aus (1):      $ \sum \limits_{1}^{n} a_{0} + a_{1} \sum \limits_{1}^{n} x_{i} = \sum \limits_{... ...hfill \Rightarrow \quad \quad \quad ~ n ~ a_{0} + a_{1} \sum x_{i} = \sum y_{i}$


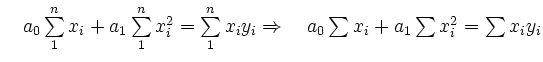
aus (2): $ \quad a_{0} \sum \limits_{1}^{n} x_{i} + a_{1} \sum \limits_{1}^{n} x_{i}^2 = ... ...hfill \Rightarrow \quad a_{0} \sum x_{i} + a_{1} \sum x_{i}^2 = \sum x_{i}y_{i}$


hier:


aus      $ ~5 a_{0} + 15a_{1} = 11$     und      $ 15 a_{0} + 55a_{1} = 43,9$     folgt für $ a_{1}$ und $ a_{0}$:


         $ a_{1} = 1,09$
         $ a_{0} = -3a_{1}+\frac{11}{5} = -1,07$


somit hat die Ausgleichsgerade folgende Gleichung: $ y = -1,07 + 1,09x$

(Prof. Dr. Eberhard Teufel, Dr. Norbert Röhrl)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 28.10.2006