Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Trigonometrische Integranden

Rationale Funktionen von Sinus und Cosinus

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Mit der Substitution

$\displaystyle x=\tan (t/2) $

erhält man für eine beliebige rationale Funktion $ r$

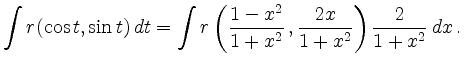
$\displaystyle \int r(\cos t, \sin t)\,dt = \int r\left(\frac{1-x^2}{1+x^2}\,, \frac{2x}{1+x^2}\right) \frac{2}{1+x^2}\,dx\,. $

Damit läßt sich ein trigonometrischer in einen rationalen Integranden überführen, der mit Partialbruchzerlegung berechnet werden kann.

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017