Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Trigonometrische Integranden

Integration mit Maple

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Bestimmte und unbestimmte Integrale erhält man in MAPLE mit dem Befehl int, wobei wenn keine Integrationsgrenzen angegeben werden, eine Stammfunktion mit Integrationskonstante 0 berechnet wird.

> int(sin(x)^2, x=0..Pi);

$\displaystyle {\displaystyle \frac {1}{2}} \,\pi $

> int(sin(x)^2, x);

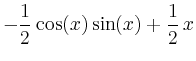
$\displaystyle - {\displaystyle \frac {1}{2}} \,\mathrm{cos}(x)\,\mathrm{sin}(x ) + {\displaystyle \frac {1}{2}} \,x $

Kann MAPLE für die Funktion keine Stammfunktion finden, so wird einfach der eingebene Ausdruck ausgegeben, man kann jedoch bestimmte Integrale numerisch berechnen lassen, indem man den Befehl evalf auf den Integral-Operator Int anwendet.

> int(exp(x^3), x=0..2);

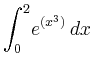
$\displaystyle {\displaystyle \int _{0}^{2}} e^{(x^{3})}\,dx $

> evalf( Int(exp(x^3), x=0..2) );

$\displaystyle 276.8528882 $

Einige Beispiele zur Bildung von Stammfunktionen in Maple sind:
> int(sin(x)^2*cos(x)^4,x);

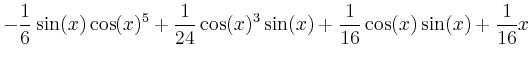
$\displaystyle -\frac{1}{6}\sin(x)\cos(x)^5+\frac{1}{24}\cos(x)^3 \sin(x)+\frac{1}{16}\cos(x) \sin(x)+\frac{1}{16}x $

> int(sin(x)^5*cos(x),x);

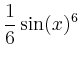
$\displaystyle \frac{1}{6}\sin(x)^6 $

> int(tan(x)^4,x);

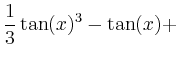$\displaystyle \frac{1}{3}\tan(x)^3-\tan(x)+$arctan$\displaystyle (\tan(x)) $

> int(tan(x)*sin(x)^2,x);

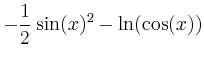
$\displaystyle -\frac{1}{2}\sin(x)^2-\ln(\cos(x)) $

(Autor: Marcus Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017