Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Numerische Integration

Trapez-Regel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Näherung

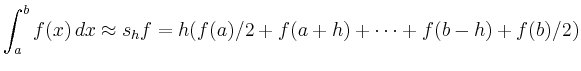
$\displaystyle \int_a^b f(x)\, dx \approx s_h f = h (f(a)/2 + f(a+h) + \cdots + f(b-h) + f(b)/2) $

approximiert das Integral durch eine Summe von Trapezflächen.

\includegraphics[width=.95\moimagesize]{trapez3}

Für eine zweimal stetig differenzierbare Funktion gilt für den Fehler:

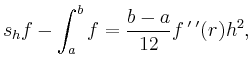
$\displaystyle s_h f - \int_a^b f = \frac{b-a}{12} f\,'\,'(r) h^2, $

für ein $ r\in[a,b]$.

Genauer besitzt der Fehler für glatte Funktionen die asymptotische Entwicklung

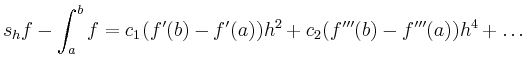
$\displaystyle s_h f - \int_a^b f = c_1(f^\prime(b)-f^\prime(a))h^2 + c_2(f^{\prime\prime\prime}(b)-f^{\prime\prime\prime}(a)) h^4 + \dots $

mit von $ f$ und $ h$ unabhängigen Konstanten $ c_j$. Daraus folgt, dass die Trapezregel für $ (b-a)$-periodische Funktionen sehr genau ist. Der Fehler strebt schneller als jede $ h$-Potenz gegen Null.

Der Fehler auf einem Intervall ist

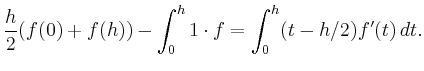
$\displaystyle \frac{h}{2} (f(0) + f(h)) - \int_0^h 1\cdot f = \int_0^h (t-h/2) f^\prime(t)\, dt. $

Nochmalige partielle Integration und Anwendung des Mittelwertsatzes ergibt

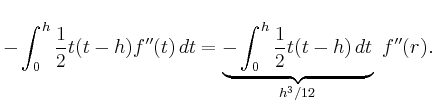
$\displaystyle -\int_0^h \frac{1}{2} t(t-h) f^{\prime\prime}(t)\, dt = \underbrace{-\int_0^h \frac{1}{2} t(t-h)\,dt}_{ h^3/12}\ f^{\prime\prime}(r). $

Nach Summation über alle Teilintervalle erhält man

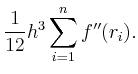
$\displaystyle \frac{1}{12}{h^3} \sum_{i=1}^n f^{\prime\prime}(r_i). $

Die Summe läßt sich durch

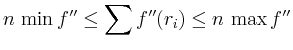
$\displaystyle n\,\min f^{\prime\prime} \le \sum f^{\prime\prime}(r_i) \le n\,\max f^{\prime\prime} $

abschätzen. Nach dem Zwischenwertsatz folgt schließlich

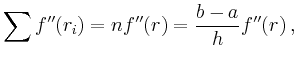
$\displaystyle \sum f^{\prime\prime}(r_i) =n f^{\prime\prime}(r) = \frac{b-a}{h}f^{\prime\prime}(r)\,, $

mit einem $ r \in [a,b]$.

Der Beweis der asymptotischen Fehlerentwicklung ist aufwändiger. Er beruht auf sukzessiver partieller Integration des Restgliedes und einer geeigneten Behandlung der Randterme.

(Autoren: Höllig/Hörner)
Die Bessel-Funktionen $ \mathcal{J}_k$ besitzen für ganzzahliges $ k$ die Integraldarstellung

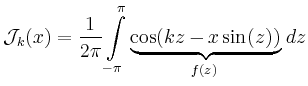
$\displaystyle \mathcal{J}_k(x) = \frac{1}{2\pi} \int\limits_{-\pi}^{\pi} \underbrace{\cos(kz-x\sin(z))}_{f(z)}\,dz $

und sind für $ k = 0,\ldots ,4$ in der folgenden Abbildung dargestellt.

\includegraphics[width=0.5\linewidth]{Trapezregel_Bessel.eps}

Bei der Berechnung mit der Trapez-Regel nutzt man aus, dass

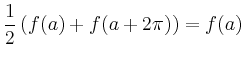
$\displaystyle \frac{1}{2}\left(f(a)+f(a+2\pi)\right) = f(a) $

und dass $ f$ gerade ist. Wählt man die Punkte

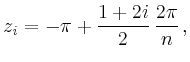
$\displaystyle z_{\mathit i} = -\pi+\frac{1+2i}{2}\, \frac{2\pi}{n}\,, $

so ist die Summe

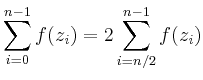
$\displaystyle \sum\limits_{i=0}^{n-1} f(z_{\mathit i}) = 2\sum\limits_{i=n/2}^{n-1} f(z_{\mathit i}) $

zu bilden.

Wie die Folge der Approximationen von $ \mathcal{J}_1(2)$ mit $ n=4,8, \ldots 64$ Punkten zeigt, ist die Konvergenz äußerst schnell.

\begin{tabular}{r\vert l} $n$\ & \\ \hline & \\ [-1.5ex] 4 & \underline{0}.4546... ... & \\ [-1.5ex] 64 &\underline{0.57672480775687338720244824226913} \end{tabular}

Diese hohe Genauigkeit der Trapezregel ist typisch für glatte periodische Integranden und kann mit einer genaueren Darstellung des Fehlers, der Euler-Maclaurinschen Summenformel, begründet werden.

(Autoren: Höllig/Hörner)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017