Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Numerische Integration

Gauß-Formel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Gauß-Formel der Ordnung $ n$ approximiert das Integral einer Funktion durch das Integral des Interpolationspolynoms an den Nullstellen $ x_1<\cdots < x_n$ des Legendre-Polynoms vom Grad n:

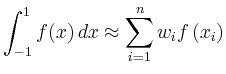
$\displaystyle \int_{-1}^{1} f(x)\, dx \approx \sum_{i=1}^{n} w_i f \left( x_i \right) $

mit $ w_i$ den Integralen der Lagrange-Polynome

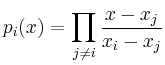
$\displaystyle p_i (x) = \prod_{j \neq i} \frac{x-x_j}{x_i-x_j} $

über das Intervall $ \left[ -1,1 \right]$.

Die Formel ist exakt für Polynome vom Grad$ <2n$ und vor allem für analytische Funktionen sehr genau. Alle Gewichte $ w_i$ sind positiv, und die Stützstellen $ x_i$ liegen im Integrationsintervall $ (-1, 1)$. Diese Gauß-Parameter sind tabelliert und bis zur Ordnung 10 in der folgenden Tabelle angegeben.

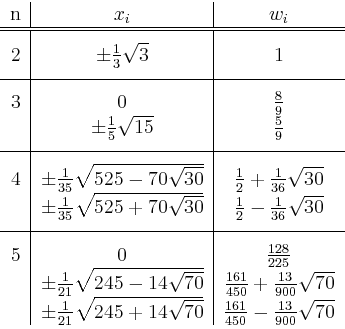
\begin{tabular}{c\vert c\vert c} n & $x_i$\ & $w_i$\ \\ \hline \hline & &\\ [-1... ...rt{245+14\sqrt{70}}$\ & $\frac{161}{450}-\frac{13}{900} \sqrt{70}$ \end{tabular}
Gauß-Parameter $ x^{'}$ und $ w^{'}$ für ein beliebiges Integrationsintervall $ [a, b]$ erhält man durch lineare Transformation:

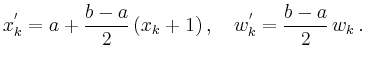
$\displaystyle x^{'}_{k} = a + \frac{b-a}{2}\,(x_k+1)\,,\quad w^{'}_{k} = \frac{b-a}{2}\,w_{k}\,. $

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017