Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Integralrechnung - Uneigentliche Integrale

Uneigentliches Integral

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine auf $ [a,b)$ stückweise stetige Funktion $ f$ wird durch

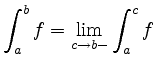
$\displaystyle \int_a^b f = \lim_{c\to b-} \int_a^c f $

der Integralbegriff auf unendliche Intervalle ($ b=\infty$ ) und unbeschränkte Integranden ( $ f(b)=\pm\infty$ ) erweitert.

Analog wird eine Singularität an der unteren oder an beiden Grenzen behandelt. Im letzteren Fall muss der Grenzwert unabhängig von der Wahl der Folgen $ c\to a+$ , $ d\to b-$ sein.

Hinreichend für die Existenz eines uneigentlichen Integrals ist die absolute Intergrierbarkeit von $ f$ , d. h.

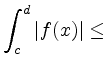$\displaystyle \int_c^d \left\vert f(x) \right\vert \leq$    const

für alle Teilintervalle $ [ c, d]\subset (a,b)$ .

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017