Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: LAAG Prüfungsvorbereitung (math./phys.) - Vektorräume

Test

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Aufgabe 1:
Es sei $ V$ ein endlich dimensionalen Vektorraum, $ U$ und $ W$ Untervektorräume von $ V$ und $ \varphi: \ V \longrightarrow V$ linear. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.

a)
Ist $ \varphi$ injektiv, so ist $ \varphi$ auch surjektiv.
b)
$ \varphi(U \cap W)=\varphi(U) \cap \varphi(W)$.
c)
$ \varphi^{-1}(W)$ ist ein Unterraum von $ V$.
d)
$ W=\varphi^{-1}(W)$.

Antwort:

  wahr falsch
a)
b)
c)
d)
Aufgabe 2:
Sei $ V$ ein Vektorraum über einem Körper $ K$. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.

a)
Sind die Vektoren $ v_1 , ... , v_n \in V$ linear abhängig, dann lässt sich $ v_1$ als Linearkombination der übrigen $ v_i$ darstellen.

b)
Sind $ n$ Vektoren $ v_1 , ... , v_n \in V$ linear abhängig, dann ist dim$ (V) < n$.

c)
Ist dim$ (V) = n$, dann sind je $ n$ Vektoren aus $ V$ stets linear abhängig.

d)
Ist dim$ (V) < n$, dann sind je $ n$ Vektoren aus $ V$ stets linear abhängig.

e)
Sind die Vektoren $ v_1$ und $ v_2$ linear abhängig, dann gibt es unendlich viele verschiedene Lösungen der Gleichung $ \lambda_1 v_1 + \lambda_2 v_2 = 0$.

f)
Sind die Vektoren $ v_1$ und $ v_2$ linear abhängig, dann gibt es unendlich viele verschiedene Lösungen der Gleichung $ \lambda_1 v_1 + \lambda_2 v_2 = 0$, falls $ K$ unendlich viele Elemente enthält.

Antwort:

  wahr falsch
a)
b)
c)
d)
e)
f)
Aufgabe 3:
Sei $ V$ ein Vektorraum über einem Körper $ K$. Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind.

Eine Teilmenge $ W \subset V$ ist ein Untervektorraum von $ V$, wenn gilt

a)
$ \forall \lambda \in K \ \forall w \in W$ :      $ \lambda w \in W$.

b)
$ \forall w_1 \, , \, w_2 \in W$ :      $ w_1 + w_2 \in W$.

c)
$ \forall \lambda \in K \ \forall w \in W$ :      $ \lambda w \in W$ und      $ \forall w_1 \, , \, w_2 \in W$ :      $ w_1 + w_2 \in W$.

d)
$ \forall \lambda_1 \, , \, \lambda_2 \in K \ \forall w_1 \, , \, w_2 \in W$ :      $ \lambda_1 w_1 + \lambda_2 w_2 \in W $.

Antwort:

  wahr falsch
a)
b)
c)
d)
Aufgabe 4:
Setzen Sie die folgenden Sätze mit jeweils einer der vorgegebenen Alternativen so fort, dass wahre Aussagen entstehen.

a)
Eine Basis eines 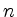$ n$-dimensionalen Vektorraums besteht aus ...

... genau 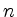$ n$ Vektoren.
... mindestens 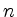$ n$ Vektoren.
... genau 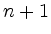$ n+1$ Vektoren.

b)
Ein Erzeugendensystem eines Vektorraums ist zugleich eine Basis dieses Vektorraums, wenn ...

... sich jedes Element des Vektorraums als eine Linearkombination der Erzeuger darstellen lässt.
... das Erzeugendensystem minimal ist.
... ein weiteres Erzeugendensystem dieses Vektorraums existiert, das weniger Elemente als das besagte System enthält.

c)
Der Basisergänzungssatz besagt, dass ...

... zu jedem Erzeugendensystem eines Vektorraums geeignete Vektoren existieren, die dieses Erzeugendensystem zu einer Basis des Vektorraums ergänzen.
... zu jedem Untervektorraum eines gegebenen Vektorraums geeignete Vektoren existieren, die eine Basis dieses Unterraums zu einer Basis des gesamten Vektorraums ergänzen.
... jede Basis eines Vektorraums zu einer entsprechenden Basis eines beliebigen anderen Vektorraums ergänzt werden kann.

Aufgabe 5:
Entscheiden Sie, ob die folgenden Aussagen über Vektoren im $ \mathbb{R}^3$ wahr oder falsch sind.

a)
Die Vektoren $ \left( \begin{array}{c} 2 \\ 0 \\ 1 \end{array} \right)$ , $ \left( \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right)$ und $ \left( \begin{array}{c} 2 \\ 1 \\ 3 \end{array} \right)$ sind linear unabhängig in $ \mathbb{R}^3$.

b)
Die Vektoren $ \left( \begin{array}{c} 2 \\ 0 \\ 1 \end{array} \right)$ , $ \left( \begin{array}{c} 0 \\ 1 \\ 3 \end{array} \right) $ und $ \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) $ bilden ein Erzeugendensystem des $ \mathbb{R}^3$.

c)
Die Vektoren $ \left( \begin{array}{c} 2 \\ 0 \\ 1 \end{array} \right)$ , $ \left( \begin{array}{c} 0 \\ 1 \\ 3 \end{array} \right) $ und $ \left( \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \right) $ bilden eine Basis des $ \mathbb{R}^3$.

d)
Die Vektoren $ \left( \begin{array}{c} 7 \\ 5 \\ 12 \end{array} \right)$ und $ \left( \begin{array}{c} 21 \\ 15 \\ 36 \end{array} \right) $ können zu einer Basis des $ \mathbb{R}^3$ ergänzt werden.

e)
Der Vektor $ \left( \begin{array}{c} 4 \\ 1 \\ 1 \end{array} \right) $ liegt in der linearen Hülle der Vektoren $ \left( \begin{array}{c} 2 \\ 1 \\ 3 \end{array} \right)$ und $ \left( \begin{array}{c} 1 \\ 2 \\ 2 \end{array} \right) $.

f)
Die Dimension des von den Vektoren $ \left( \begin{array}{c} 9 \\ -2 \\ 3 \end{array} \right) $ , $ \left( \begin{array}{c} 5 \\ 4 \\ 8 \end{array} \right)$ und $ \left( \begin{array}{c} 17 \\ -14 \\ -7 \end{array} \right)$ aufgespannten Untervektorraums des $ \mathbb{R}^3$ ist 3.

Antwort:

  wahr falsch
a)
b)
c)
d)
e)
f)
Aufgabe 6:
Sei $ K= \mathbb{Z}/ 13\mathbb{Z}$. Sind die Vektoren

\begin{displaymath}\left( \begin{array}{c} {[1]} \\ {[3]} \\ {[5]} \end{array} \... ...t( \begin{array}{c} {[1]} \\ {[1]} \\ {[1]} \end{array} \right)\end{displaymath}

in $ K^3$ linear unabhängig ?

Antwort:

wahr falsch
   
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.4.2008