
Mathematik-Online-Kurs: Lineare Algebra - Übungen - Grundlegende Strukturen

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Lineare Algebra - Übungen - Grundlegende Strukturen | |
Orthogonale Basis |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
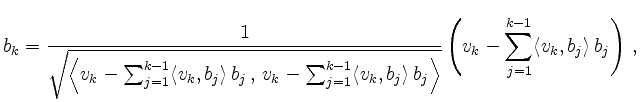
Ist ![]() auch eine Orthonormalbasis von
auch eine Orthonormalbasis von
![]() ?
?
Gegeben sind die Vektoren
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Im
![]() ist die Basis
ist die Basis
![]() mit
mit
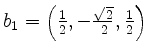 ,
,
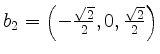 ,
,
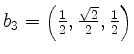
gegeben und ![]() bezeichne die Standardbasis.
bezeichne die Standardbasis.
Die lineare Abbildung ![]() ist durch
ist durch
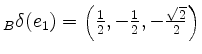 ,
,
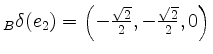 ,
,
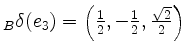
definiert.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 22.8.2008 |