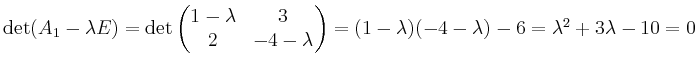
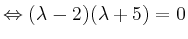 .
.
Das charakteristische Polynom
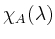 zerfällt somit in Linearfaktoren und ist damit diagonalisierbar. Die Eigenwerte lauten:
zerfällt somit in Linearfaktoren und ist damit diagonalisierbar. Die Eigenwerte lauten:
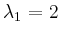 und
und
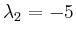 .
.
Die Diagonalmatrix ergibt sich nun aus den Eigenwerten:
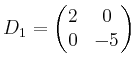
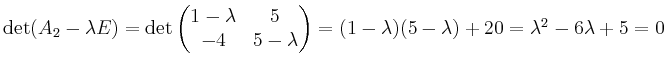
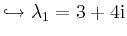 und
und
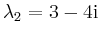 .
.
Über
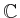 betrachtet, liegen wieder zwei verschiedene einfache Nullstellen des chrakteristischen Polynoms vor. Damit ist die Matrix komplex diagonlisierbar. Und es folgt:
betrachtet, liegen wieder zwei verschiedene einfache Nullstellen des chrakteristischen Polynoms vor. Damit ist die Matrix komplex diagonlisierbar. Und es folgt:
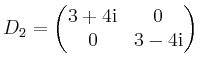
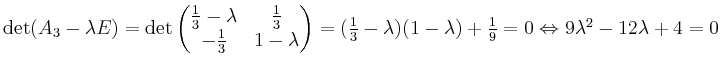 . Diese quadratische Gleichung liefert nur die doppelte Nullstelle
. Diese quadratische Gleichung liefert nur die doppelte Nullstelle
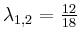 als Lösung. Da man wegen
als Lösung. Da man wegen
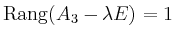 nur einen Eigenvektor zum einzigen Eigenwert
nur einen Eigenvektor zum einzigen Eigenwert 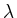 erhält, kann die Matrix
erhält, kann die Matrix 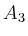 nicht diagonalisiert werden.
nicht diagonalisiert werden.
| |
automatisch erstellt
am 14.7.2008 |


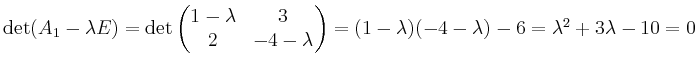
![]() .
.
![]() zerfällt somit in Linearfaktoren und ist damit diagonalisierbar. Die Eigenwerte lauten:
zerfällt somit in Linearfaktoren und ist damit diagonalisierbar. Die Eigenwerte lauten:
![]() und
und
![]() .
.
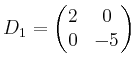
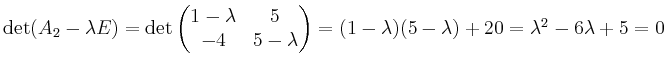
![]() und
und
![]() .
.
![]() betrachtet, liegen wieder zwei verschiedene einfache Nullstellen des chrakteristischen Polynoms vor. Damit ist die Matrix komplex diagonlisierbar. Und es folgt:
betrachtet, liegen wieder zwei verschiedene einfache Nullstellen des chrakteristischen Polynoms vor. Damit ist die Matrix komplex diagonlisierbar. Und es folgt:
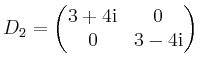
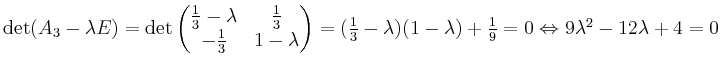 . Diese quadratische Gleichung liefert nur die doppelte Nullstelle
. Diese quadratische Gleichung liefert nur die doppelte Nullstelle
![]() als Lösung. Da man wegen
als Lösung. Da man wegen
![]() nur einen Eigenvektor zum einzigen Eigenwert
nur einen Eigenvektor zum einzigen Eigenwert ![]() erhält, kann die Matrix
erhält, kann die Matrix ![]() nicht diagonalisiert werden.
nicht diagonalisiert werden.