Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Mathematische Grundlagen - Aussagenlogik

Logische Verknüpfungen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Logische Aussagen können durch die in der folgenden Tabelle angegebenen Operationen verknüpft werden.

Bezeichnung Schreibweise (Sprechweise) wahr, genau dann wenn
Negation $ \lnot A$ (nicht $ A$) $ A$ falsch ist
Konjunktion $ A\land B$ ($ A$ und $ B$) $ A$ und $ B$ wahr sind
Disjunktion $ A\lor B$ ($ A$ oder $ B$) $ A$ oder $ B$ wahr ist
Antivalenz $ A \not\equiv B$ (entweder $ A$ oder $ B$) $ A$ und $ B$ unterschiedliche Wahrheitswerte haben
Implikation
$ A\Rightarrow B$  
$ B\Leftarrow A$  
(aus $ A$ folgt $ B$)  
($ B$ folgt aus $ A$)  
$ A$ falsch oder $ B$ wahr ist
Äquivalenz $ A\Leftrightarrow B$ ($ A$ ist äquivalent zu $ B$) $ A$ und $ B$ den gleichen Wahrheitswert haben

Um in logischen Ausdrücken Klammern zu sparen, wird festgelegt, dass $ \lnot$ stärker bindet als $ \land$ sowie $ \lor$ und diese wiederum stärker als $ \Rightarrow$, $ \Leftrightarrow$ sowie $ \not\equiv$.

Bei der Implikation ist zu beachten, dass $ B$ nur dann wahr sein muss, wenn $ A$ wahr ist. Aus falschen Voraussetzungen können sowohl richtige, als auch falsche Schlüsse gezogen werden.

Das Zeichen für die Oder-Verknüpfung ist ein stilisiertes v, das für vel (lat. oder) steht. Für die Oder-Verknüpfung wird auch das ,,$ +$``-Symbol verwendet und für die Und-Verknüpfung das ,,$ \cdot$``-Symbol. Verwendet man dann die 0 für den Wert ,,falsch`` und interpretiert jeden anderen Wert als ,,wahr``, können die logischen Verknüpfungen durch Rechnen mit natürlichen Zahlen durchgeführt werden.

Vor allem in Computersprachen werden die aus dem Englischen stammenden Begriffe NOT (Negation), AND (Konjunktion), OR (Disjunktion), EXOR oder XOR (exclusive or, Antivalenz) und deren Negationen NAND (negierte Konjunktion), NOR (negierte Disjunktion) und NXOR (Äquivalenz) verwendet.

In der folgenden Tabelle sind die Wahrheitswerte der vorgestellten Verknüpfungen angegeben. Dabei steht $ w$ für wahr und $ f$ für falsch.

$ A$ $ B$ $ \lnot A$ $ A\land B$ $ A\lor B$ $ A \not\equiv B$ $ A\Rightarrow B$ $ A\Leftrightarrow B$
w w f w w f w w
w f f f w w f f
f w w f w w w f
f f w f f f w w
Stellt man Aussagen als Schalter dar, die geschlossen sind, falls die Aussage wahr ist beziehungsweise geöffnet sind, wenn die Aussage falsch ist, so kann die Und-Verknüpfung durch eine Serienschaltung und die Oder-Verknüpfung durch eine Parallelschaltung realisiert werden.
Und-Verknüpfung Oder-Verknüpfung
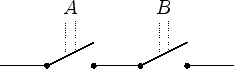\includegraphics{logische_schaltungen_und} \includegraphics[origin=tl]{logische_schaltungen_oder}

Eine negierte Aussage entspricht einem Schalter, der geschlossen ist, falls die Aussage falsch ist. Damit lassen sich auch Schaltbilder für die Äquivalenz, Antivalenz und Implikation angeben.

Äquivalenz: $ A \Leftrightarrow B$ bzw. $ (A \land B) \lor (\lnot A \land \lnot B)$
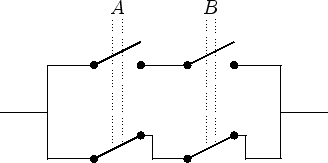\includegraphics{logische_schaltungen_gleich}
Antivalenz: $ A \not\equiv B$ bzw. $ (A \land \lnot B) \lor (\lnot A \land B)$
\includegraphics[origin=tl]{logische_schaltungen_ungleich}
Implikation: $ A \Rightarrow B$ bzw. $ \lnot A \lor B$
\includegraphics[origin=tl]{logische_schaltungen_implikation}

Die Schalter können z.B. durch Transistoren realisiert werden, die bei einer hohen oder niedrigen angelegten Spannung leiten. Der Wert w entspricht einer hohen Spannung (1), der Wert f einer niedrigen Spannung (0).

In DIN 40900 werden Symbole für die entsprechenden Schaltungen definiert. Diese bestehen aus Rechtecken, in denen die jeweilige Verknüpfung angegeben wird. Eine Negation wird durch einen Kreis gekennzeichnet.

Konjunktion Disjunktion Antivalenz
\includegraphics[width=0.25\moimagesize]{din_und} \includegraphics[width=0.25\moimagesize]{din_oder} \includegraphics[width=0.25\moimagesize]{din_exor}
Negation Implikation Äquivalenz
\includegraphics[width=0.25\moimagesize]{din_not} \includegraphics[width=0.25\moimagesize]{din_implikation} \includegraphics[width=0.25\moimagesize]{din_gleich}

(Autor: J. Hörner)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011