Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Mathematische Grundlagen - Reelle Zahlen

Normalisierte Gleitpunktzahl

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Eine $ p$-stellige normalisierte Gleitpunktzahl zur Basis $ \beta$,

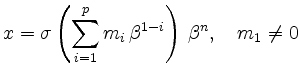
$\displaystyle x = \sigma \left( \sum _{i=1}^{p} m_i\,\beta^{1-i} \right)\,\beta^n, \quad m_1\neq 0 $

besteht aus einem Vorzeichen $ \sigma=\pm 1$, einer Mantisse $ m$ mit $ m_i\in\{0,\ldots,\beta-1\}$ und einem Exponenten $ n$ mit $ n_{\text{min}}\leq n\leq n_{\text{max}}$.

Die kleinste und größte Gleitpunktzahl sind

$\displaystyle x_{\min}=\beta^{n_{\text{min}}},\quad x_{\max}=\beta^{n_{\text{max}}+1}(1-\beta^{-p})\,. $

Da $ m_1\neq 0$ ist, kann die Zahl 0 nicht als normalisierte Gleitpunktzahl dargestellt werden.

Neben der dezimalen Darstellung ($ \beta=10$), werden auch die Dualdarstellung ($ \beta=2$) und Hexadezimaldarstellung ($ \beta=16$) häufig in der Praxis verwendet.

(Inhalt vorübergehend nicht verfügbar)

Eine Gleitpunktzahl mit doppelter Genauigkeit wird als Gleitpunktzahl in Dualdarstellung mit einem transformierten Exponenten,

$\displaystyle x=\pm 1.m_2\cdots m_p\cdot 2^{n-1023}, $

abgespeichert. Für den IEEE-Standard werden 53bit für das Vorzeichen und die Mantisse und 11bit für den Exponenten $ n$ benötigt:


0  1       11 12                                   63
$ \sigma$    $ n$    $ m_2$        $ \cdots$                $ m_{53}$

Die Exponenten $ \underline{n}=0$ und $ \overline{n}=2047$ sind Spezialfälle. Daher ist

$\displaystyle x_{\min}=2^{-1022},\quad x_{\max}=(1-2^{-53})2^{1024} $

die kleinste und größte positive Zahl, die mit doppelter Genauigkeit dargestellt werden kann.

Die Darstellung für spezielle Fälle wird in der folgenden Tabelle gezeigt.


$ \sigma$ $ n$ $ m$
0 0 oder 1 $ \underline{n}=0$ 0
underflow 0 oder 1 $ \underline{n}$ $ m_1=0$
overflow (Inf) 0 oder 1 $ \overline{n}=2047$ $ m_2=m_3=\ldots =0$
NaN 0 oder 1 $ \overline{n}$ $ m_2$ oder $ m_3$ oder $ \ldots\ne 0$

Underflow entsteht für $ \vert x\vert<x_{\min}$. Der Exponent $ \underline{n}$ wird in diesem Fall zur Darstellung weiterer, nicht normalisierter ($ m_1=0$) Gleitpunktzahlen genutzt. Damit erhält man den zusätzlichen Zahlenbereich

$\displaystyle 0.1\cdots 1\cdot 2^{-1022}\geq x\geq 0.0\cdots 01\cdot 2^{-1022} = 2^{-1074}\,. $

Die Zahl $ 2^{-1075}$ ist nicht mehr darstellbar und wird nach 0 gerundet.

Overflow entsteht für $ \vert x\vert>x_{\max}$ und wird durch das Symbol Inf und ein Vorzeichen dargestellt.

Man erhält NaN, das für not-a-number steht, bei einer nicht definierten Rechenoperation, wie z.B. 0/0, Inf-Inf, etc.

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.5.2011