Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vektorrechnung - Ebenen

Parameterdarstellung einer Ebene

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Punkte $ X$ auf einer Ebene durch $ P$ , die von zwei nicht parallelen Richtungen $ \vec{u}$ und $ \vec{v}$ aufgespannt wird, erfüllen

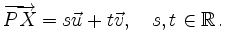
$\displaystyle \overrightarrow{PX} = s\vec{u}+t\vec{v},\quad s,t\in\mathbb{R}\, . $

\includegraphics[width=10cm]{param_darst}

Entsprechend gilt

$\displaystyle x_i = p_i + su_i+tv_i,\quad i=1,2,3\, . $

für die Koordinaten des Ortsvektors $ \vec{x}$ .
Eine Ebene E sei gegeben durch den Punkt $ P=(1, 2, 3)$ und die Vektoren $ \vec{u} = (2,0,0)^t$ und $ \vec{v} = (1,1,1)^t$ , d.h.

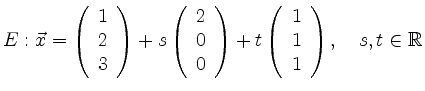
$\displaystyle E: \vec{x} =\left(\begin{array}{c}1\\ 2\\ 3\end{array}\right)+s\l... ...)+t\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right),\quad s,t \in \mathbb{R} $

Dann liegt $ X = (1,1,2)$ auf der Ebene, denn es gilt

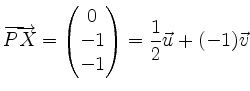
$\displaystyle \overrightarrow{PX} = \begin{pmatrix}0\\ -1 \\ -1\\ \end{pmatrix} = \frac{1}{2} \vec{u} + (-1) \vec{v} $

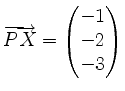Andererseits liegt $ X = (0,0,0)$ nicht auf der Ebene, denn es ist $ \overrightarrow{PX} = \begin{pmatrix}-1\\ -2 \\ -3\\ \end{pmatrix}$ und das Gleichungssystem

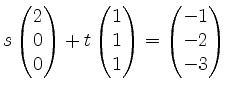
$\displaystyle s \begin{pmatrix}2\\ 0 \\ 0\\ \end{pmatrix} + t \begin{pmatrix}1\\ 1 \\ 1\\ \end{pmatrix} = \begin{pmatrix}-1\\ -2 \\ -3\\ \end{pmatrix} $

hat keine Lösung, wie man an der zweiten und dritten Zeile sehen kann.

(Autoren: Höllig/Weiß )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 17.3.2011