Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vektorrechnung - Ebenen

Hesse-Normalform einer Ebene

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Ortsvektor $ \vec{x}$ eines Punktes $ X$ auf einer Ebene durch $ P$ orthogonal zu einem Normalenvektor $ \vec{n}$ erfüllt

$\displaystyle \vec{x}\cdot\vec{n} = d,\,\quad d=\vec{p}\cdot\vec{n}\, . $

Bei der Normalform wird dabei $ \vert\vec{n}\vert=1$ und $ d\ge0$ angenommen. In diesem Fall ist $ d$ der Abstand der Ebene zum Ursprung.

\includegraphics[width=10cm]{hesse_form}
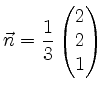Eine Ebene $ E$ sei gegeben durch den Punkt $ P=(1, 2, 3)$ und den normierten Normalenvektor $ \vec{n} = \dfrac{1}{3} \begin{pmatrix}2\\ 2\\ 1\\ \end{pmatrix}$ .

Es ist

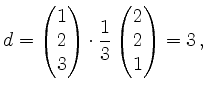
$\displaystyle d = \begin{pmatrix}1\\ 2\\ 3\\ \end{pmatrix}\cdot \frac{1}{3} \begin{pmatrix}2\\ 2\\ 1\\ \end{pmatrix} = 3\, , $

d.h. die Ebene hat die Normalform

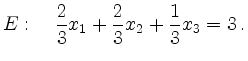
$\displaystyle E: \quad \frac{2}{3}x_1+\frac{2}{3}x_2+\frac{1}{3}x_3=3\,. $

Dann liegt $ X=(4,0,1)$ auf der Ebene, denn es gilt

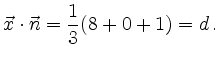
$\displaystyle \vec{x} \cdot \vec{n} = \frac{1}{3}(8+0+1) = d\, . $

Andererseits liegt $ X = (0,0,0)$ nicht auf der Ebene, denn es ist

$\displaystyle \vec{x} \cdot \vec{n} = 0 \neq d \, .$

(Autoren: Höllig/Weiß )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 17.3.2011