

Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven | ||
Ellipse | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
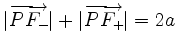
mit
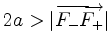 .
.
![\includegraphics[width=12.4cm]{a_ellipse}](/inhalt/aussage/aussage480/img5.png)
Ist
![]() , so gilt für die
Koordinaten
, so gilt für die
Koordinaten
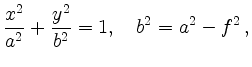
und
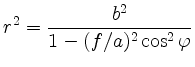
für die Polarkoordinaten der Punkte
Eine Parametrisierung der Ellipse ist
mit
Um zu zeigen, dass
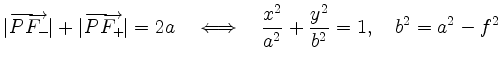
quadriert man
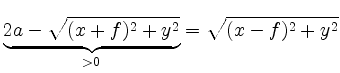
und erhält die zur linken Gleichung äquivalente Beziehung
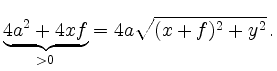
Erneutes Quadrieren nach Division durch
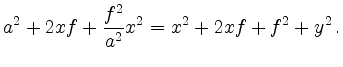
Mit Substitution von
Zur Herleitung der Polarform
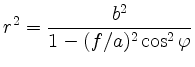
multipliziert man mit dem Nenner und berücksichtigt
Damit folgt
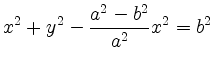
und Division durch
![\includegraphics[
width=10.4cm
]{b_brennpunktstrahlen}](/inhalt/beispiel/beispiel334/img1.png)
Zum Beweis wählt man als Hilfspunkte das
Spiegelbild ![]() des Brennpunkts
des Brennpunkts ![]() an der Tangente
an der Tangente ![]() und
einen beliebigen Punkt
und
einen beliebigen Punkt ![]() auf
auf ![]() .
Da
.
Da ![]() außerhalb der Ellipse liegt, ist
außerhalb der Ellipse liegt, ist
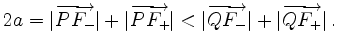
Ersetzt man die Strecken
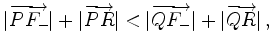
und folglich müssen
Diese Spiegelungseigenschaft wird bei der
Zertrümmerung von Nierensteinen ausgenutzt.
Die Strahlen aus einer radialen Quelle im
Brennpunkt ![]() können durch einen elliptischen
Reflektor im Brennpunkt
können durch einen elliptischen
Reflektor im Brennpunkt ![]() gebündelt werden.
gebündelt werden.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 17.3.2011 |