

Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven | ||
Parabel | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
![\includegraphics[
width=12.4cm
]{a_parabel}](/inhalt/aussage/aussage481/img4.png)
Ist ![]() und
und ![]() , so gilt für die
Koordinaten
, so gilt für die
Koordinaten
und
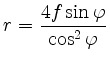
für die Polarkoordinaten der Punkte
Die Äquivalenz der Darstellungen ist offensichtlich. Durch Gleichsetzen der quadrierten Abstände,
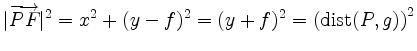
erhält man die Koordinatenform. Substitution von
führt auf die Polarform.
![\includegraphics[
width=12.4cm
]{b_satellitentv}](/inhalt/beispiel/beispiel335/img1.png)
Zum Beweis bemerkt man, dass
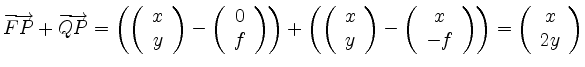
parallel zur Richtung der Tangente im Punkt
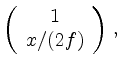
ist. Da
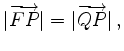
folgt daraus die Gleichheit der Winkel
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 17.3.2011 |