

Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vektorrechnung - Quadratische Kurven | ||
Hyperbel | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
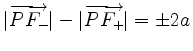
mit
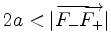 .
.
![\includegraphics[
width=8.4cm
]{a_hyperbel}](/inhalt/aussage/aussage482/img5.png)
Ist
![]() , so gilt für die
Koordinaten
, so gilt für die
Koordinaten
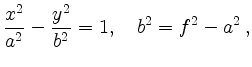
und
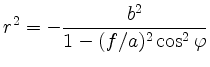
für die Polarkoordinaten der Punkte
Parametrisierungen der Hyperbeläste sind
mit
Um zu zeigen, dass
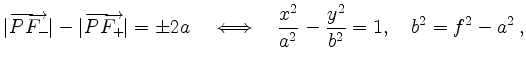
quadriert man
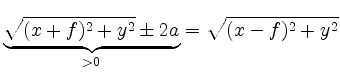
und erhält die zur linken Gleichung äquivalente Beziehung
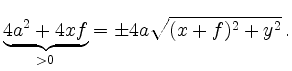
Erneutes Quadrieren nach Division durch
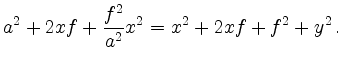
Mit Substitution von
Zur Herleitung der Polarform
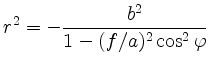
multipliziert man mit dem Nenner und berücksichtigt
Damit folgt
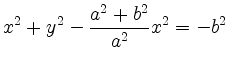
und Division durch
![\includegraphics[
width=9cm
]{b_navigation}](/inhalt/beispiel/beispiel336/img6.png)
Als konkretes Beispiel wird
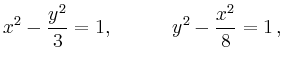
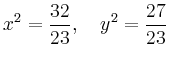
Wie auch aus der Abbildung ersichtlich ist, existieren vier Lösungen. Bei der Navigation ist dies unproblematisch, da ein Kapitän wissen sollte, wo sich sein Schiff ungefähr befindet, d.h. welches die relevante Lösung ist.
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 17.3.2011 |