Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vektorrechnung - Vektoren

Skalarmultiplikation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Vektor $ s\vec{a}$ entspricht einer $ s$ -fachen Verschiebung, d.h.

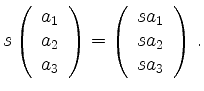
$\displaystyle s\left(\begin{array}{c}a_1\\ a_2\\ a_3\end{array}\right) = \left(\begin{array}{c}sa_1\\ sa_2\\ sa_3\end{array}\right)\, . $

Speziell ist $ 0\vec{a}=\vec{0}$ .
\includegraphics[width=7.4cm]{a_smult.eps}
Die Seitenhalbierenden in einem Dreieck schneiden sich im Schwerpunkt $ S$ mit dem Ortsvektor

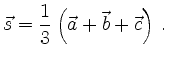
$\displaystyle \vec{s}= \frac{1}{3} \left(\vec{a} + \vec{b} + \vec{c} \right) \,. $

\includegraphics[width=7.4cm]{bsp_seitenhalb}

Um dies zu verifizieren schreibt man die Ortsvektoren der Punkte auf der Seitenhalbierenden $ \overline{AM_a}$ in der Form

$\displaystyle \vec{p}=\vec{a}+t(\vec{m}_a-\vec{a})=\vec{a} +t\left(\frac{1}{2}\vec{b}+\frac{1}{2}\vec{c}-\vec{a}\right), \quad t \in \left[0,1\right]. $

Für $ t=2/3$ ist $ \vec{p}=\vec{s}$ ; der Schwerpunkt teilt also $ \overline{AM_a}$ im Verhältnis $ 2:1$ . Entsprechendes gilt für die Seitenhalbierenden $ \overline{BM_b}$ und $ \overline{CM_c}$ .

(Autoren: Höllig/Much)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 17.3.2011