Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Vektorräume

Unterraum

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine nichtleere Teilmenge $ U$ eines $ K$-Vektorraums $ V$, die mit der in $ V$ definierten Addition und Skalarmultiplikation selbst einen Vektorraum bildet, nennt man einen Unterraum von $ V$.

Unterräume $ U$ werden oft durch Bedingungen an die Elemente von $ V$ definiert:

$\displaystyle U = \{v \in V: A(v)\}, $

wobei $ A$ eine Aussage bezeichnet, die für $ v \in V$ erfüllt sein muss.

Um zu prüfen, ob es sich bei einer nichtleeren Teilmenge $ U$ von $ V$ um einen Unterraum handelt, genügt es zu zeigen, dass $ U$ bzgl. der Addition und Skalarmultiplikation abgeschlossen ist:

$\displaystyle u,v \in U$ $\displaystyle \implies$ $\displaystyle u+v \in U$  
$\displaystyle \lambda \in K, u \in U$ $\displaystyle \implies$ $\displaystyle \lambda \cdot u \in U\,.$  

(Autoren: App/Kimmerle)
Unterräume entstehen oft durch Spezifizieren zusätzlicher Eigenschaften. Betrachtet man den Vektorraum der reellen Funktionen

$\displaystyle f:\,\mathbb{R}\to\mathbb{R}\, , $

so bilden beispielsweise die geraden Funktionen ( $ f(x) = f(-x)$ für alle $ x\in\mathbb{R}$) einen Unterraum. Weitere Beispiele bzw. Gegenbeispiele sind in der folgenden Tabelle angegeben:

Eigenschaft Unterraum
ungerade ja
beschränkt ja
monoton nein
stetig ja
positiv nein
linear ja

(Autoren: App/Höllig)
Für jeden Vektor $ d\ne 0$ eines $ K$-Vektorraums bildet die durch 0 verlaufende Gerade

$\displaystyle v = \lambda d,\quad \lambda\in K $

einen Unterraum.

Allerdings ist eine Gerade, die nicht durch 0 verläuft, kein Unterraum. Beispielsweise liegt $ (1,0)^{\operatorname t}$ auf der Geraden

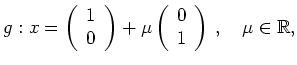
$\displaystyle g: x= \left(\begin{array}{c}1\\ 0 \end{array}\right) + \mu\left(\begin{array}{c}0\\ 1 \end{array}\right) \,,\quad\mu\in\mathbb{R}, $

$ (2,0)^{\operatorname t}$ jedoch nicht.
(Autoren: App/Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009