Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Quadratische Kurven

Hyperbel

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für die Punkte $ P=(x,y)$ auf einer Hyperbel ist die Differenz der Abstände zu zwei Brennpunkten $ F_{\pm}$ konstant:

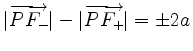
$\displaystyle \vert\overrightarrow{PF_-}\vert - \vert\overrightarrow{PF_+}\vert = \pm 2 a $

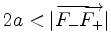mit $ 2a<\vert\overrightarrow{F_-F_+}\vert$ .

\includegraphics[ width=8.4cm ]{a_hyperbel}

Ist $ F_{\pm}=(\pm f,0)$ , so gilt für die Koordinaten

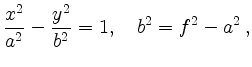
$\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1,\quad b^2 = f^2 - a^2\, , $

und

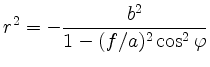
$\displaystyle r^2 = -\frac{b^2}{1-(f/a)^2\cos^2\varphi} $

für die Polarkoordinaten der Punkte $ P$ . Die Asymptoten haben die Steigung $ \pm b/a$ .

Parametrisierungen der Hyperbeläste sind

$\displaystyle x=\pm a \cosh t,\quad y=b\sinh t $

mit $ t\in\mathbb{R}$ .

Die Äquivalenz der Darstellungen kann man durch direktes Nachrechnen überprüfen.

Um zu zeigen, dass

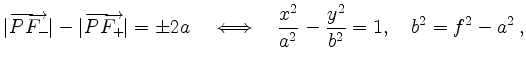
$\displaystyle \vert\overrightarrow{PF_-}\vert - \vert\overrightarrow{PF_+}\vert... ...{\displaystyle{\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1}},\quad b^2 = f^2 - a^2\,,$

quadriert man

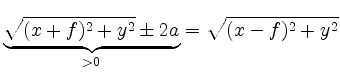
$\displaystyle \underbrace{\sqrt{(x+f)^2 + y^2}\pm 2a}_{> 0} = \sqrt{(x-f)^2 + y^2} $

und erhält die zur linken Gleichung äquivalente Beziehung

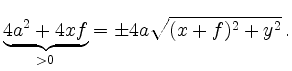
$\displaystyle \underbrace{4a^2 + 4xf}_{>0} = \pm 4a \sqrt{(x+f)^2 + y^2}\, . $

Erneutes Quadrieren nach Division durch $ 4a$ liefert

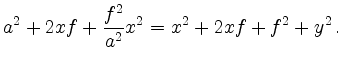
$\displaystyle a^2 + 2xf + \frac{f^2}{a^2} x^2 = x^2 + 2xf + f^2 + y^2\, . $

Mit Substitution von $ f^2 = a^2+b^2$ ergibt sich nach Umformung die Koordinatenform.

Zur Herleitung der Polarform

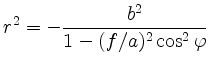
$\displaystyle r^2 = -\frac{b^2}{1-(f/a)^2\cos^2 \varphi } $

multipliziert man mit dem Nenner und berücksichtigt

$\displaystyle x^2 = (x^2 + y^2)\cos^2 \varphi\, . $

Damit folgt

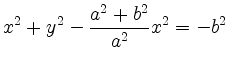
$\displaystyle x^2 + y^2 - \frac{a^2+b^2}{a^2} x^2 = -b^2 $

und Division durch $ -b^2$ ergibt die Koordinatenform.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009