Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Lineare Algebra und Geometrie - Quadratische Kurven

Navigation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Zur Bestimmung der Position $ P$ eines Schiffes werden die Zeitdifferenzen $ 2 a_{j,k}$ beim Empfang von synchronen Radiosignalen von verschiedenen Sendestationen $ F_i$ verglichen. So lässt sich $ P$ als Schnittpunkt der Hyperbeln mit Brennpunkten $ F_j$, $ F_k$ bestimmen.

\includegraphics[ width=9cm ]{b_navigation}

Als konkretes Beispiel wird

$\displaystyle F_1 = (-2,0),\, F_2 = (2,0),\quad F_3 = (0,-3),\, F_4 = (0,3) $

und $ a_{1,2} = a_{3,4} = 1$ gewählt. Die entsprechenden Hyperbelgleichungen sind

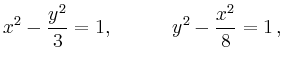
$\displaystyle x^2 - \frac{y^2}{3} = 1,\qquad\quad y^2 - \frac{x^2}{8} = 1\, , $

und man erhält

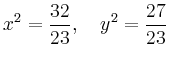
$\displaystyle x^2 = \frac{32}{23},\quad y^2 = \frac{27}{23} $

für die Koordinaten der möglichen $ 4$ Schnittpunkte $ S_i$.

Wie auch aus der Abbildung ersichtlich ist, existieren vier Lösungen. Bei der Navigation ist dies unproblematisch, da ein Kapitän wissen sollte, wo sich sein Schiff ungefähr befindet, d.h. welches die relevante Lösung ist.

(Autoren: App/Höllig )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009