Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Kombinatorik

Permutationen und symmetrische Gruppe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für eine beliebige Menge $ M$ bilden die Bijektionen von $ M$ in $ M$, versehen mit der Komposition von Abbildungen als Operation, eine Gruppe, die sogenannte symmetrische Gruppe von $ M$.

Ist $ M = \{1, 2, \dots, n\}$, so spricht man von der symmetrischen Gruppe $ S_n$ vom Grad $ n$. Die $ n!$ Elemente $ \pi$ von $ S_n$ nennt man Permutationen und benutzt die Schreibweise

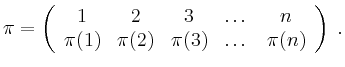
$\displaystyle \pi=\left( \begin{array}{ccccc} 1 & 2 & 3 & \dots & n \\ \pi(1) & \pi(2) & \pi(3) & \dots & \pi(n) \end{array} \right) \; . $

Dabei stehen in der oberen Zeile die Elemente der Menge in der natürlichen Reihenfolge, darunter dann jeweils ihre Bilder unter $ \pi$.

Die Permutationsgruppe ist im Allgemeinen nicht kommutativ.

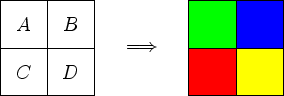
\includegraphics{quadrat}

Ein Quadrat das in die vier Felder $ A,B,C,D$ unterteilt ist soll mit den Farben Rot, Blau, Grün und Gelb so ausgemalt werden, dass je zwei Felder unterschiedlich gefärbt sind. Es gibt dann $ 4!=1 \cdot 2 \cdot 3 \cdot 4=24$ verschiedene Farbgestaltungen.

(Aus: Vorkurs Mathematik)
Die folgende Tabelle zeigt alle Permutationen von $ \{1,2,3\}$:
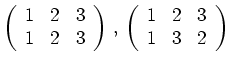    $\displaystyle \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \end{array} \right)\,,\, \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \end{array} \right)$  
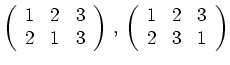    $\displaystyle \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \end{array} \right)\,,\, \left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array} \right)$  
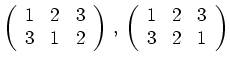    $\displaystyle \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \end{array} \right)\,,\, \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array} \right)$  

Im allgemeinen ist die Hintereinanderschaltung von Permutationen nicht kommutativ. Beispielsweise erhält man für

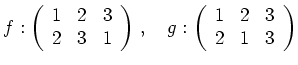
$\displaystyle f: \left(\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \end{array}\... ...uad g: \left(\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \end{array}\right) $

die Verknüpfungen:
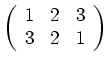$\displaystyle f \circ g$ $\displaystyle :$ $\displaystyle \left(\begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array}\right)$  
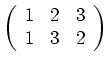$\displaystyle g \circ f$ $\displaystyle :$ $\displaystyle \left(\begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \end{array}\right)$  

(Autoren: Höllig/Knesch)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009