Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Kombinatorik

Fakultät

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Produkt der ersten $ n$ natürlichen Zahlen wird mit

$\displaystyle n! = 1\cdot 2 \cdots n $

bezeichnet (lies: $ n$ Fakultät). Konsistent mit der Definition des leeren Produktes setzt man $ 0!=1$.

Die Zahl $ n!$ entspricht der Anzahl der verschiedenen Möglichkeiten $ n$ unterschiedliche Objekte anzuordnen.

Für großes $ n$ kann das asymptotische Verhalten von $ n!$ mit Hilfe der Stirlingschen Formel approximiert werden:

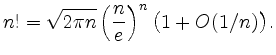
$\displaystyle n! = \sqrt{2\pi n}\left(\frac{n}{e}\right)^n\big(1+ O(1/n)\big)\,. $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009