Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Kombinatorik

Kombinatorik von Mengen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Die folgende Tabelle gibt die Anzahl der Möglichkeiten an, aus einer Menge mit $ n$ verschiedenen Elementen $ k$ Elemente auszuwählen, wobei unterschieden werden muß, ob die Reihenfolge eine Rolle spielt (sortiert) und Wiederholungen zugelassen sind.

  sortiert nicht sortiert
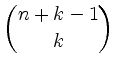mit Wiederholungen $ n^k$ $ \displaystyle \binom{n+k-1}{k}$
ohne Wiederholungen $ n(n-1)\cdots(n-k+1)$ $ \displaystyle \binom{n}{k}$

i)
unsortierte Auswahl ohne Wiederholungen

Berücksichtigt man die Reihenfolge, so gibt es $ n$ Möglichkeiten für das erste, $ (n-1)$ Möglichkeiten für das zweite, bis hin zu $ (n-k+1)$ Möglichkeiten für das $ k$-te Element, also insgesamt

$\displaystyle n(n-1)\cdots(n-k+1) $

Möglichkeiten. Diese Anzahl muß noch durch die Anzahl

$\displaystyle k! $

der Permutationen von $ k$ Elementen dividiert werden.

ii)
unsortierte Auswahl mit Wiederholungen

Ein äquivalentes Problem ist, $ n-1$ Markierungen zwischen $ n+k$ Punkten zu plazieren.

$ \bullet$ | $ \bullet$ | $ \bullet$ | $ \bullet$ | $ \bullet$ | $ \bullet$ | $ \bullet$ | $ \bullet$
          $ \vartriangle$   $ \vartriangle$       $ \vartriangle$   $ \vartriangle$  
Die um $ 1$ verminderte Anzahl der Punkte zwischen der $ (i-1)$-ten und $ i$-ten Markierung entspricht den Wiederholungen des $ i$-ten Elements. Nach i) ergibt sich für die Anzahl der möglichen Markierungen

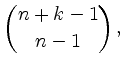
$\displaystyle \binom{n+k-1}{n-1}\, , $

was mit der in der Tabelle angegebenen Zahl übereinstimmt.

iii)
Die Formeln für die sortierte Auswahl ergeben sich unmittelbar.
(Autoren: Höllig/Knesch)
In einer Urne befinden sich eine rote, eine grüne und eine blaue Kugel. In der Tabelle sieht man die Anzahl der Möglichkeiten bei zweimaligem Ziehen ($ n=3$, $ k=2$).

  sortiert nicht sortiert
mit Wiederholungen
(mit Zurücklegen)
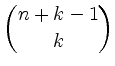$ n^k$ $ \displaystyle \binom{n+k-1}{k}$
  \includegraphics[width=.21\linewidth]{moeglichkeit1} \includegraphics[width=.21\linewidth]{moeglichkeit3}
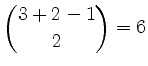  $ 3^2=9$ $ \displaystyle \binom{3+2-1}{2}=6$
ohne Wiederholungen
(ohne Zurücklegen)
$ n(n-1)\cdots(n-k+1)$ $ \displaystyle \binom{n}{k}$
  \includegraphics[width=.21\linewidth]{moeglichkeit2} \includegraphics[width=.135\linewidth]{moeglichkeit4}
  $ 3\cdot 2 = 6$ $ \displaystyle \binom{3}{2}=3$
(Autoren: Höllig/Knesch)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009