Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Kombinatorik

Zerlegung einer natürlichen Zahl

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Auf wie viele verschiedene Arten lässt sich die Zahl $ m$ als Summe von $ n$-Zahlen $ a_i \geq 0$ schreiben, wobei die Reihenfolge zu beachten ist? Es wird also die Anzahl der $ (a_1, a_2, \ldots , a_n)$ mit $ a_i \geq 0$ und

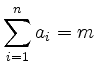
$\displaystyle \sum_{i=1}^na_i =m $

gesucht.

Um die Frage zu lösen stellt man sich die Zahl $ m$ als eine Folge von $ m$ Kästchen vor:

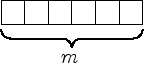
\includegraphics{summe_kasten1}
An diese $ m$ Kästchen werden nun $ n-1$ Kästchen angehängt:
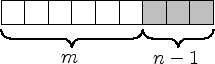
\includegraphics{summe_kasten2}
Von diesen $ m+n-1$ Kästchen werden nun $ n-1$ beliebige Kästchen entfernt, z.B.
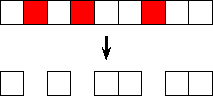
\includegraphics{summe_kasten3}

Das Ergebnis sind insgesamt $ m$ Kästchen die in $ n$ Blöcke zerlegt sind. Die vorangegangen Bilder sind ein Beispiel für die Zerlegung von $ m=6$ in $ n=4$ Zahlen und entspricht der Zerlegung $ a_1=1,a_2=1,a_3=2,a_4=2$ also $ 6=1+1+2+2$.

Es sind noch die folgenden Sonderfälle zu beachten:

Man sieht, dass unterschiedliche Arten die Kästchen zu entfernen auch unterschiedliche Zerlegungen liefern. Außerdem lässt sich jede Zerlegung von $ m$ in dieser Art darstellen. Es gibt also genau so viele Zerlegungen der Zahl $ m$ in eine Summe von $ n$ Zahlen $ a_i \geq 0$, wie es Möglichkeiten gibt aus einer $ m+n-1$-elementigen Menge eine $ n-1$-elementige Teilmenge zu wählen, also ist die Anzahl

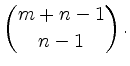
$\displaystyle \binom{m+n-1}{n-1} \,. $

(Aus: Vorkurs Mathematik)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009