Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Gleichungen und Ungleichungen

Quadratische Gleichung

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Eine quadratische Gleichung hat die Form

$\displaystyle ax^2+bx+c=0 \textnormal{, }\qquad a\not=0. $

und wird mit der sogenannten Mitternachtsformel gelöst:

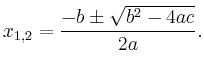
$\displaystyle x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}. $

Der Term $ D = b^2 - 4ac$ wird Diskriminante genannt. Am Vorzeichen der Diskriminante kann die Anzahl der reellen Lösungen einer quadratischen Gleichung erkannt werden. Man erhält für

Mit Hilfe der Lösungen lässt sich die Gleichung als Linearfaktorzerlegung schreiben:

$\displaystyle a(x-x_{1})(x-x_{2})=0. $

(Autor: Jahn)
Für die Gleichung

$\displaystyle 5x^2-5x-30=0 $

erhält man mit der Mitternachtsformel

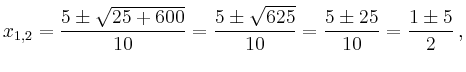
$\displaystyle x_{1,2}=\frac{5\pm\sqrt{25+600}}{10} =\frac{5\pm\sqrt{625}}{10} =\frac{5\pm25}{10} =\frac{1\pm5}{2}\,, $

also die Lösungen

$\displaystyle x_{1}=3 \qquad x_{2}=-2\,. $

Die Linearfaktorzerlegung lautet

$\displaystyle 5(x-3)(x+2)=0\,. $

(Autor: Jahn)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009