Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Gleichungen und Ungleichungen

Polynomdivision

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Zu Polynomen $ p$ und $ q$ mit $ m=$Grad$ \,q\le$Grad$ \,p=n$ gibt es eindeutig bestimmte Polynome $ f$ und $ r$ mit

$\displaystyle p = fq + r,$   Grad$\displaystyle \,f = n-m,\,$   Grad$\displaystyle \,r < m\, . $

Diese Zerlegung kann durch Division mit Rest bestimmt werden.

Speziell folgt für eine Nullstelle $ t$ von $ p$ dass $ p(x) = f(x)(x-t)$ mit Grad$ \,f=n-1$ .

Division von $ p$ durch $ q$ ergibt

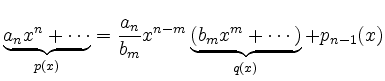
$\displaystyle \underbrace{a_n x^n + \cdots}_{p(x)} = \frac{a_n}{b_m} x^{n-m} \underbrace{(b_m x^m + \cdots)}_{q(x)} + p_{n-1}(x) $

mit einem Rest $ p_{n-1}(x) = a^\prime_{n-1} x^{n-1}+\cdots$ .

Ist $ m\le n-1$ kann erneut dividiert werden:

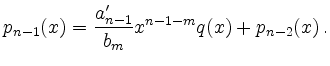
$\displaystyle p_{n-1}(x) = \frac{a_{n-1}^\prime}{b_m} x^{n-1-m} q(x) + p_{n-2}(x)\, . $

Die Prozedur bricht ab, wenn der Grad des Restpolynoms kleiner als $ m$ ist, d.h. spätestens mit

$\displaystyle r = p_{n-(n-m+1)}\, . $

Durch sukzessives Einsetzen der Produkte folgt

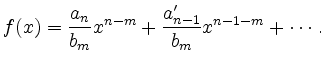
$\displaystyle f(x) = \frac{a_n}{b_m} x^{n-m}+ \frac{a_{n-1}^\prime}{b_m} x^{n-1-m} + \cdots\, . $

Ist $ t$ Nullstelle von $ p$ , so gilt

$\displaystyle 0=p(t)=f(t)(t-t)+r(t) = r(t) $

und somit $ r(x)=0$ , da Grad$ \,r < 1$ .

(Autoren: Höllig/Hörner)
Die Polynomdivision kann analog zur schriftlichen Division durchgeführt werden. Beispielsweise erhält man für $ p(x)=9x^5+12x^4+10x^3+4x^2+4x+2$ und $ q(x)=3x^2+2x+1$

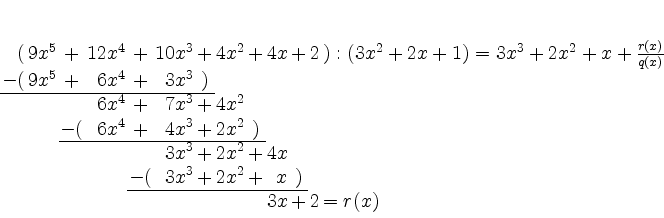
\begin{displaymath}\setlength{\arraycolsep}{.2ex} \begin{array}{rr*{5}{cr}l} ... ... x&)\\ \cline{5-11} & & & & & & & & &3x&+&2& =r(x) \end{array}\end{displaymath}

Es ist also

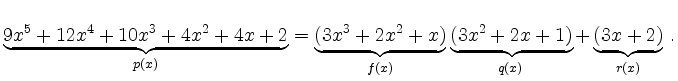
$\displaystyle \underbrace{9x^5+12x^4+10x^3+4x^2+4x+2}_{p(x)}=\underbrace{(3x^3+2x^2+x)}_{f(x)} \underbrace{(3x^2+2x+1)}_{q(x)}+\underbrace{(3x+2)}_{r(x)}\,. $

(Autoren: Höllig/Hörner)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009