Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Grundlagen - Komplexe Zahlen

Division komplexer Zahlen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Der Quotient $ z_1/z_2$ zweier komplexer Zahlen

$\displaystyle z_k = x_k + \mathrm{i} y_k = r_k \exp(\mathrm{i}\varphi_k) $

ist

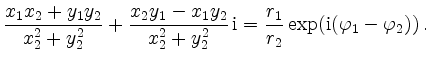
$\displaystyle \frac{x_1x_2+y_1y_2}{x_2^2+y_2^2} + \frac{x_2y_1-x_1y_2}{x_2^2+y_2^2}\,\mathrm{i} = \frac{r_1}{r_2}\exp(\mathrm{i}(\varphi_1-\varphi_2))\, . $

Speziell ist

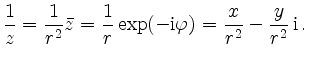
$\displaystyle \frac{1}{z} = \frac{1}{r^2} \bar z = \frac{1}{r} \exp(-\mathrm{i}\varphi) = \frac{x}{r^2} - \frac{y}{r^2}\,\mathrm{i} \,. $

Der Kehrwert einer komplexen Zahl läßt sich durch Spiegelung am Einheitskreis $ C$ konstruieren, wie in der Abbildung veranschaulicht ist.

\includegraphics[height=6cm]{a_division_bild}

Die komplex konjugierte Zahl $ w=\bar z$ ist der Schnittpunkt der Diagonalen des Vierecks aus den Tangenten an $ C$ durch den Punkt $ z$ und den rechtwinklig schneidenden Radii. Die Zahl $ z$ erhält man dann durch Spiegelung an der reellen Achse.

Mit $ z_k = x_k + \mathrm{i} y_k = r_k \exp (i \varphi_k)$ gilt für den Quotient zweier komplexer Zahlen:

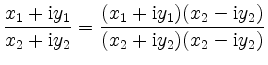$\displaystyle \frac{z_1}{z_2}$ $\displaystyle =$ $\displaystyle \frac{x_1+\mathrm{i} y_1 }{x_2 + \mathrm{i} y_2 } = \frac{(x_1 +\mathrm{i}y_1)(x_2-\mathrm{i}y_2)} {(x_2+\mathrm{i}y_2)(x_2-\mathrm{i}y_2)}$  
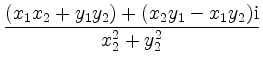  $\displaystyle =$ $\displaystyle \frac{(x_1x_2+y_1y_2) + (x_2y_1 - x_1y_2)\mathrm{i}} {x_2^2+y_2^2}$  

bzw.

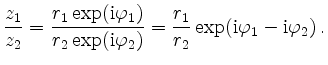
$\displaystyle \frac{z_1}{z_2} = \frac{r_1 \exp (\mathrm{i} \varphi_1)}{r_2 \ex... ..._2)} = \frac{r_1}{r_2} \exp (\mathrm{i} \varphi_1 - \mathrm{i} \varphi_2)\, . $

Insbesondere erhält man

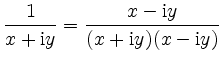$\displaystyle \frac{1}{z}$ $\displaystyle =$ $\displaystyle \frac{1}{x + \mathrm{i} y} = \frac {x - \mathrm{i} y}{(x + \mathrm{i} y)(x - \mathrm{i}y)}$  
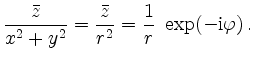  $\displaystyle =$ $\displaystyle \frac{\bar {z}}{x^2+y^2} = \frac{\bar{z}}{r^2} = \frac{1}{r} \ \exp(-\mathrm{i} \varphi) \,.$  

Die geometrische Konstruktion basiert auf dem Theorem von Pythagoras. Daraus folgt

$\displaystyle \vert w\vert\,\vert z\vert = 1^2 \,, $

d.h. $ w$ hat den korrekten Betrag. Spiegelung an der reellen Achse ändert dann das Vorzeichen des Arguments, so dass

$\displaystyle \operatorname{arg} \bar w = \operatorname{arg} (1/z) $

wie behauptet.

(Autoren: Höllig/Kopf)
Um

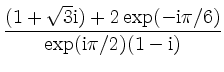
$\displaystyle \frac{(1+\sqrt{3}\mathrm{i})+2 \exp (-\mathrm{i}\pi/6)}{\exp(\mathrm{i}\pi/2) (1-\mathrm{i})} $

zu berechnen, bildet man die Summe im Zähler mit der Standardform,

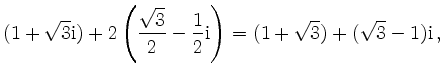
$\displaystyle (1+\sqrt{3}\mathrm{i})+ 2\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\mathrm{i} \right) = (1+\sqrt{3})+(\sqrt{3}-1)\mathrm{i}\, , $

und das Produkt im Nenner mit der Polarform,

$\displaystyle \exp(\mathrm{i}\pi/2)\cdot \sqrt{2}\exp(-\mathrm{i}\pi/4) = \sqrt{2}\exp(\mathrm{i}\pi/4) = 1 + \mathrm{i}\, . $

Damit ist der Quotient

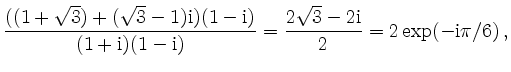
$\displaystyle \frac{((1+\sqrt{3})+(\sqrt{3}-1)\mathrm{i}) (1-\mathrm{i})}{(1+\m... ...thrm{i})} = \frac{2\sqrt{3} - 2\mathrm{i}}{2} = 2 \exp(-\mathrm{i}\pi/6)\, , $

und die Umwandlung in Standardform ergibt

$\displaystyle 2(\cos(\pi/6)-\mathrm{i}\sin(\pi/6)) = \sqrt{3}-\mathrm{i} \,. $

(Autoren: Höllig/Kopf)
Für die Analyse linearer Wechselstromnetzwerke ist die komplexe Schreibweise vorteilhaft. Schreibt man für die Spannung und Stromstärke

$\displaystyle U(t) = U_0 e^{\mathrm{i}(\omega t+\varphi)}\,, \quad I(t) = I_0 e^{\mathrm{i}(\omega t+\psi)}\,, $

so ist der komplexe Widerstand

$\displaystyle Z = U(t)/I(t) $

zeitunabhängig. Für die Grundelemente

Widerstand $ R$   Spule $ L$   Kondensator $ C$        
\includegraphics[width=.2\moimagesize]{komplexe_zahlen_schaltelement_widerstand.eps}      \includegraphics[width=.2\moimagesize]{komplexe_zahlen_schaltelement_induktivitaet.eps}      \includegraphics[width=.2\moimagesize]{komplexe_zahlen_schaltelement_kapazitaet.eps}        
$ Z=R$   $ Z=\mathrm{i}\omega L$   $ Z=(\mathrm{i}\omega C)^{-1}$        
addieren sich die komplexen Widerstände bei Serienschaltung:

$\displaystyle Z_{\text{gesamt}} = Z_1 + Z_2 $

und ihre Kehrwerte bei Parallelschaltung:

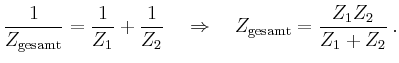
$\displaystyle \frac{1}{Z_{\text{gesamt}}} = \frac{1}{Z_1} + \frac{1}{Z_2} \quad \Rightarrow \quad Z_{\text{gesamt}}=\frac{Z_1 Z_2}{Z_1+Z_2}\, . $

Man bezeichnet $ \operatorname{Re} Z$ als Wirkwiderstand, $ \operatorname{Im} Z$ als Blindwiderstand und $ \vert Z\vert$ als Scheinwiderstand oder Impedanz.

Beispielsweise beträgt für den Schaltkreis

\includegraphics[width=.6\moimagesize]{komplexe_zahlen_schaltkreis.eps}
der Gesamtwiderstand

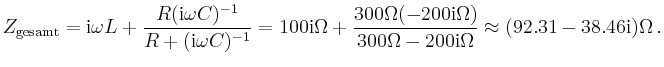
$\displaystyle Z_{\text{gesamt}}=\mathrm{i}\omega L+ \frac{R(\mathrm {i}\omega... ...}{300\Omega-200\mathrm {i}\Omega}\approx (92.31 -38.46\mathrm{i})\Omega \,. $

Bei einer Wechselspannung von $ U_{\text{effektiv}}=220$V fließt dabei ein Effektivstrom von

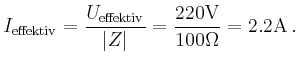
$\displaystyle I_{\text{effektiv}}=\frac{U_{\text{effektiv}}}{\vert Z\vert}=\frac{220\mathrm{V}}{100\Omega}=2.2\mathrm{A} \,. $

(Autoren: Höllig/Wipper)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009