Überprüfen Sie sowohl durch Umformung, als auch mit Hilfe einer
Wahrheitswerttabelle, ob die Ausdrücke
Tautologien sind.
(Autoren: Hörner/Lesky)
Die Platzhalter
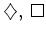 stehen jeweils für eine der logischen
Operatoren aus der Menge
stehen jeweils für eine der logischen
Operatoren aus der Menge
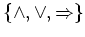 . In welchen Fällen gilt dann
. In welchen Fällen gilt dann
(Autor: Joachim Wipper)
Vereinfachen Sie die folgende Schaltung:
(Autor: Jörg Hörner)
Gegeben sind die Mengen
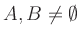 , eine Abbildung
, eine Abbildung
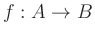 sowie die Teilmengen
sowie die Teilmengen
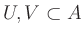 und
und
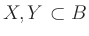 . Zeigen bzw. widerlegen Sie mit Hilfe eines geeigneten
Gegenbeispiels die folgenden Beziehungen:
. Zeigen bzw. widerlegen Sie mit Hilfe eines geeigneten
Gegenbeispiels die folgenden Beziehungen:
(Autor: Joachim Wipper)
Drücken Sie die folgenden Aussagen über eine Abbildung
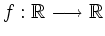 in formaler Schreibweise aus:
in formaler Schreibweise aus:
| a) |
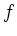 ist nicht surjektiv
ist nicht surjektiv |
| b) |
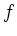 ist nicht injektiv
ist nicht injektiv |
| c) |
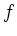 ist nicht bijektiv
ist nicht bijektiv |
| d) |
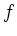 ist weder surjektiv noch injektiv
ist weder surjektiv noch injektiv |
(Autor: Christian Apprich)
Beweisen Sie mit vollständiger Induktion für
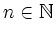 :
:
a)
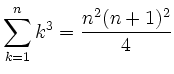
|
| b)
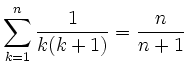
|
(Aus: HM I WS 1997/1998)
Beweisen Sie mit Hilfe vollständiger Induktion für
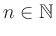 :
:
- a)
-
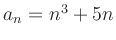 ist durch
ist durch  teilbar.
teilbar.
- b)
-
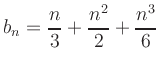 ist eine natürliche Zahl.
ist eine natürliche Zahl.
(Autoren: Boßle/Wipper)
Auf einer Party treffen sich 25 Personen. Wie viele Hände werden geschüttelt, wenn jeder Gast jedem anderen
die Hand gibt.
(Aus: Vorkurs Mathematik)
Beweisen Sie:
a)
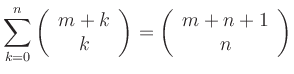
b)
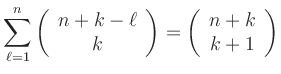
(Autor: Klaus Höllig)
Wie viele Möglichkeiten gibt es, beim Pokerspiel mit 32 Karten
(8 Werte in 4 Farben)
ein Full-House (drei gleiche Werte und zwei gleiche Werte) zu erhalten?
Wie viele Möglichkeiten gibt es dafür, dass sich das abgebildete Blatt
durch Tausch von zwei Karten auf einen Poker (vier gleiche Werte) verbessert?
(Autoren: Höllig/Hörner)
Geben Sie für folgende komplexe Zahlen eine Darstellung der Form
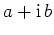 mit
mit
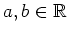 an:
an:
(Aus: HM I 1992-1998)
Bestimmen Sie folgende Teilmengen von
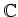 und skizzieren Sie diese in
der Gaußschen Zahlenebene:
und skizzieren Sie diese in
der Gaußschen Zahlenebene:
(Aus: HM I WS 97/98)
| |
automatisch erstellt
am 23.10.2009 |




![\includegraphics[width=.5\linewidth]{V005_bild}](/inhalt/aufgabe/aufgabe25/img1.png)
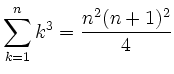
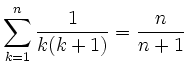
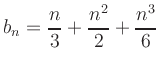 ist eine natürliche Zahl.
ist eine natürliche Zahl.
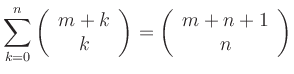 b)
b)
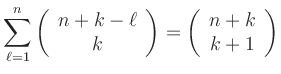

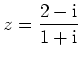
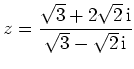
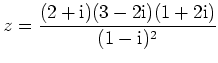
![$ {\displaystyle{z = \frac{\left[{\textstyle{2(\cos
\frac{\pi}{12}+{\rm {i}}\sin...
...eft[{\textstyle{4(\cos
\frac{\pi}{4}+{\rm {i}}\sin \frac{\pi}{4})}}\right]^3}}}$](/inhalt/aufgabe/aufgabe5/img8.png)