Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Differentialrechnung

Babylonisches Wurzelziehen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die schon von den Babyloniern verwendete Iteration

$\displaystyle x \longleftarrow (x+a/x)/2$

zur Berechnung der Wurzel einer positiven Zahl $ a$ stellt sich bei genauerer Betrachtung als das Newton-Verfahren für $ f(x)=x^2-a$ heraus:

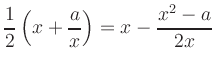
$\displaystyle \frac{1}{2}\left(x+\frac{a}{x}\right)=x-\frac{x^2-a}{2x} $

Für $ a=2, x_0=1$ erhält man die Approximationen
1
1.5
1.416666666666666666666666666666666666667
1.414215686274509803921568627450980392157
1.414213562374689910626295578890134910117
1.414213562373095048801689623502530243615
1.414213562373095048801688724209698078570

Die Konvergenz ist äußerst schnell. Bei jedem Schritt verdoppelt sich die Anzahl der korrekten Stellen (unterstrichen) annähernd. Die quadratische Konvergenz lässt sich in diesem Beispiel auch durch einfache Umformung nachweisen:

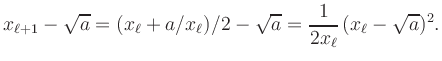
$\displaystyle x_{\ell+1}-\sqrt{a} = (x_\ell+a/x_\ell)/2-\sqrt{a} = \frac{1}{2x_\ell}\,(x_\ell-\sqrt{a})^2. $

Die geometrische Interpretation des Newton-Verfahrens zeigt, dass die Iteration für alle $ x_0 \neq 0$ konvergent ist.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 23.10.2009