

Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Extremwerte und Kurvendiskussion

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |

|
|
Mathematik-Online-Kurs: Vorkurs Mathematik - Analysis - Extremwerte und Kurvendiskussion | ||
Extrema | ||
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Bei einem lokalen Minimum ist der Funktionswert
Globales und lokales Maximum sind analog definiert.
![\includegraphics[width=0.6\linewidth]{Beispiel_Extrema.eps}](/inhalt/aussage/aussage40/img7.png)
Für eine stückweise stetig differenzierbare Funktion auf einem abgeschlossenen Intervall können Extremwerte nur an den Nullstellen der Ableitung, Unstetigkeitsstellen oder Randpunkten auftreten. Der Typ kann mit Hilfe höherer Ableitungen und durch Vergleichen der Funktionswerte ermittelt werden.
Die Funktion
![]() mit
mit
![]() besitzt zwei Minima und
ein Maximum. Das Minimum mit dem kleineren Funktionswert ist das globale.
Ein globales Maximum existiert nicht, da
besitzt zwei Minima und
ein Maximum. Das Minimum mit dem kleineren Funktionswert ist das globale.
Ein globales Maximum existiert nicht, da
![]() für
für
![]() .
.
Die Funktion ![]() mit
mit
![]() besitzt keine
Extremwerte.
besitzt keine
Extremwerte.
![\includegraphics[width=7.4cm]{Extrema_1}](/inhalt/beispiel/beispiel989/img7.png)
![\includegraphics[width=7.4cm]{Extrema_2}](/inhalt/beispiel/beispiel989/img8.png)
Ist eine Funktion auf einem offenen Intervall konstant, so sind diese Stellen sowohl (lokale) Maxima als auch (lokale) Minima.
Bei einer strikt monotonen Funktion werden die Extremwerte an den Randpunkten angenommen, falls diese zum Definitionsgebiet gehören.
![\includegraphics[width=7.4cm]{Extrema_3}](/inhalt/beispiel/beispiel989/img9.png)
![\includegraphics[width=7.4cm]{Extrema_4}](/inhalt/beispiel/beispiel989/img10.png)
Die geradlinige Strecke soll so gebaut werden, dass ein möglichst schnelles Erreichen der
Stadt gewährleistet ist, wenn von einer Durchschnittsgeschwindigkeit von
![]() km/h auf der Autobahn und
km/h auf der Autobahn und ![]() km/h auf der neuen Nebenstrecke
ausgegangen wird.
km/h auf der neuen Nebenstrecke
ausgegangen wird.
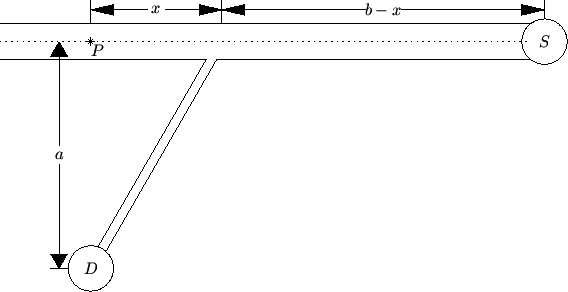
Zu bestimmen ist die Entfernung ![]() zwischen
zwischen ![]() und dem Übergang der
Nebenstrecke auf die Autobahn durch Minimierung der benötigten Zeit
und dem Übergang der
Nebenstrecke auf die Autobahn durch Minimierung der benötigten Zeit
für die Fahrt in die Stadt.
Nullsetzen der Ableitung
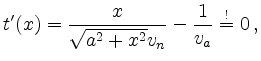
ergibt
als mögliche lokale Extremstelle in (0, b). Ob es sich um das Minimum handelt, muss durch Vergleich mit den Fahrzeiten für die Intervallendpunkte geprüft werden:
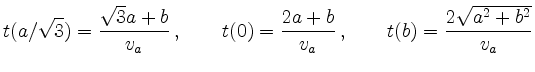
Offensichtlich ist
![]() . Für den rechten Endpunkt gilt
. Für den rechten Endpunkt gilt
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 23.10.2009 |