Mathematik-Online: Hermitesch, unitär, normal

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online:
	Hermitesch, unitär, normal

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Übersicht

Begriffe.

Sei $n\geq 1$ , sei $A\in\mathbb{C}^{n\times n}$ . Schreiben wir $A = (a_{i,j})_{i,j}$ , so sei $\bar{A} := (\bar{a}_{i,j})_{i,j} \in\mathbb{C}^{n\times n}$ .

heißt normal, falls $\bar A^\mathrm{t} A = A \bar A^\mathrm{t}$ .
heißt unitär, falls $\bar A^\mathrm{t} A = \mathrm{E}$ .
heißt hermitesch, falls $\bar A^\mathrm{t} = A$ .

Ist unitär, so ist normal. Ist hermitesch, so ist normal.

Es ist unitär genau dann, wenn die Spalten von eine Orthonormalbasis von $\mathbb{C}^n$ bilden.

Es ist hermitesch genau dann, wenn die Einträge an den bezüglich der Hauptdiagonalen gespiegelten Positionen bis auf Konjugation übereinstimmen. Insbesondere, ist hermitesch, so hat auf der Diagonalen reelle Einträge.

Es heißt unitär diagonalisierbar, wenn es eine unitäre Matrix $U\in\mathbb{C}^{n\times n}$ gibt mit $\bar U^\mathrm{t} A U = D$ diagonal.

Ist unitär diagonalisierbar, so ist insbesondere diagonalisierbar.

ist normal genau dann, wenn unitär diagonalisierbar ist.
ist unitär genau dann, wenn unitär diagonalisierbar ist und die resultierende Diagonalmatrix Diagonaleinträge vom Betrag aufweist.
ist hermitesch genau dann, wenn unitär diagonalisierbar ist und die resultierende Diagonalmatrix reelle Diagonaleinträge aufweist.

Der Beweis von ersterer Aussage benötigt die folgenden beiden Aussagen, die auch für sich genommen von Interesse sein können.

Für jede Matrix $A\in\mathbb{C}^{n\times n}$ gibt es eine unitäre Matrix $U\in\mathbb{C}^{n\times n}$ derart, daß $\bar U^\mathrm{t} A U$ eine obere Dreiecksmatrix ist (Lemma von Schur).
Eine normale obere Dreiecksmatrix ist diagonal.

Unitäres Diagonalisieren.

Sei $A\in\mathbb{C}^{n\times n}$ normal. Um eine unitäre Matrix $U\in\mathbb{C}^{n\times n}$ so zu finden, daß $\bar U^\mathrm{t} A U = D$ diagonal ist, verfahren wir wie folgt.

(1): Bestimme das charakteristische Polynom in der Form $\chi_A(X) = (X-\lambda_1)^{m_1}\cdots(X-\lambda_r)^{m_r}$ , wobei $\lambda_1, \ldots, \lambda_r$ die paarweise verschiedenen Eigenwerte der Matrix sind.
(2): Führe die Schritte (3), (4) und (5) für jedes $i\in\{1,\ldots,r\}$ durch.
(3): Berechne eine Basis $(y_1,\dots,y_{m_i})$ von $\mathrm{E}_A(\lambda_i) = \operatorname{Kern }(A - \lambda_i E)$ .
(4): Wende Gram-Schmidt an, um aus $(y_1,\dots,y_{m_i})$ eine Orthonormalbasis $(x_1,\dots,x_{m_i})$ von $\operatorname{Kern }(A - \lambda_i E)$ zu gewinnen.
(5): Trage das Tupel $(x_1,\dots,x_{m_i})$ als Spalten in die Matrix ein.

Zur Probe verifizieren wir sowie unitär. Insbesondere ist es eine oft aufschlußreiche Probe, zu verifizieren, daß Eigenvektoren verschiedener Eigenräume zueinander orthogonal sind; dies ist bei normalen Matrizen nämlich stets der Fall.

Definitheit.

Sei $A\in\mathbb{C}^{n\times n}$ . Sei $\mathrm{q}_A:\mathbb{C}^n\longrightarrow\mathbb{R}$ , $x\mapsto\mathrm{q}_A(x) := \bar x^\mathrm{t} A x$ die zu gehörige quadratische Form.

Sei nun hermitesch.

heißt positiv definit, falls $\mathrm{q}_A(x) > 0$ für alle $x\in\mathbb{C}^n\setminus\{ 0\}$ .
heißt positiv semidefinit, falls $\mathrm{q}_A(x) \geq 0$ für alle $x\in\mathbb{C}^n$ .
heißt negativ definit, falls $\mathrm{q}_A(x) < 0$ für alle $x\in\mathbb{C}^n\setminus\{ 0\}$ .
heißt negativ semidefinit, falls $\mathrm{q}_A(x) \leq 0$ für alle $x\in\mathbb{C}^n$ .
heißt indefinit, falls $\mathrm{q}_A(x) > 0$ für ein $x\in\mathbb{C}^n$ und $\mathrm{q}_A(y) < 0$ für ein $y\in\mathbb{C}^n$ .

Kurz, ist negativ (semi-)definit genau dann, wenn positiv (semi-)definit ist. Und es ist indefinit genau dann, wenn weder positiv semidefinit noch negativ semidefinit ist.

Anwendung der Definition auf die Standardbasisvektoren zeigt, daß eine positiv definite Matrix positive Hauptdiagonaleinträge, und eine negativ definite Matrix negative Hauptdiagonaleinträge aufweist.

Aber Vorsicht, es ist z.B. 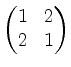$\begin{pmatrix}1&2\\ 2&1\end{pmatrix}$ trotz positiver Hauptdiagonaleinträge nicht positiv definit, sondern vielmehr indefinit (warum?).

Umgekehrt aber, gibt es einen positiven und einen negativen Hauptdiagonaleintrag in , so ist indefinit.

Wir erinnern daran, daß eine hermitesche Matrix ausschließlich reelle Eigenwerte besitzt.

Das folgende Eigenwertkriterium kann alle Fälle unterscheiden.

ist positiv definit, falls alle ihre Eigenwerte sind.
ist positiv semidefinit, falls alle ihre Eigenwerte $\geq 0$ sind.
ist negativ definit, falls alle ihre Eigenwerte sind.
ist negativ semidefinit, falls alle ihre Eigenwerte $\leq 0$ sind.
ist indefinit, falls einer ihrer Eigenwerte und einer ihrer Eigenwerte ist.

Stehen die Eigenwerte nicht zur Verfügung, so kann man stattdessen das charakteristische Polynom $\chi_A(X) = X^n + h_{n-1} X^{n-1} + \cdots + h_0 X^0\in\mathbb{R}[X]$ heranziehen.

ist positiv definit, falls $(-1)^{n-j} h_j > 0$ stets.
ist positiv semidefinit, falls $(-1)^{n-j} h_j \geq 0$ stets.
ist negativ definit, falls stets.
ist negativ semidefinit, falls $h_j \geq 0$ stets.
ist indefinit, falls weder positiv semidefinit noch negativ semidefinit ist

Sei $1\leq k\leq n$ . Schreiben wir $A = (a_{i,j})_{1\leq i\leq n,1\leq j\leq n}$ , so sei

$\displaystyle A_k \; :=\; (a_{i,j})_{1\leq i\leq k,1\leq j\leq k} \;\in\; \mathbb{C}^{k\times k}$

die $k\times k$ -Matrix im linken oberen Eck von

. Es heißt $\det A_k$ der -te Hauptminor von

Das folgende Hauptminorenkriterium erkennt nur Definitheit, nicht Semidefinitheit.

ist positiv definit, falls $\det A_k > 0$ für alle $1\leq k\leq n$ .
ist negativ definit, falls $(-1)^k\det A_k > 0$ für alle $1\leq k\leq n$ .

Das Hauptminorenkriterium für die negative Definitheit besagt also, daß die Vorzeichen der Hauptminoren alternieren, angefangen mit einem negativen Vorzeichen.

Signatur.

Sei $\mathrm{pos}(A)$ die Anzahl der positiven Eigenwerte von , sei $\mathrm{neg}(A)$ die Anzahl der negativen Eigenwerte von , jeweils gezählt mit algebraischer Vielfachheit. Unter der Signatur von versteht man das Paar $(\mathrm{pos}(A),\mathrm{neg}(A))$ .

Die hermitesche Matrix $A\in\mathbb{C}^{n\times n}$ ist positiv definit genau dann, wenn ihre Signatur gleich ist; sie ist positiv semidefinit genau dann, wenn ihre Signatur von der Form ist mit $0\leq k\leq n$ ; sie ist negativ definit genau dann, wenn ihre Signatur gleich ist; sie ist negativ semidefinit genau dann, wenn ihre Signatur von der Form ist mit $0\leq k\leq n$ ; sie ist indefinit, wenn ihre Signatur von der Form ist mit $k,\, l\,\geq\, 1$ .

Sei $S\in\mathrm{GL}_n(\mathbb{C})$ . Der Sylvestersche Trägheitssatz besagt, daß und $\bar S^\mathrm{t} A S$ dieselbe Signatur haben. Dies ermöglicht es uns, die Signatur von mit folgendem beidseitigen Gaußalgorithmus zu berechnen.

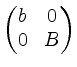Zunächst formen wir mit folgenden Schritten um zu einer Matrix der Gestalt $\begin{pmatrix}b&0\\ 0&B\end{pmatrix}$ , mit $b\in\mathbb{C}$ und $B\in\mathbb{C}^{(n-1)\times (n-1)}$ .

(1): Ist der Eintrag an Position gleich Null für $j\in\{2,\dots,n\}$ , so sind wir fertig.
(2): Ist der Eintrag an Position ungleich Null, so gehe zu (4).
(3): Bestimme ein $j\in\{2,\dots,n\}$ mit einem Eintrag an Position ungleich Null und addiere die -te Zeile zur ersten Zeile, und die -te Spalte zur ersten Spalte.
(4): Addiere für alle $j\in\{2,\dots,n\}$ ein Vielfaches der ersten Zeile auf die -te Zeile so, daß der Eintrag an Position annulliert wird.
(5): Trage für alle $j\in\{2,\dots,n\}$ eine 0 an der Position ein.

Diese Prozedur führe man nun erneut für die hermitesche Matrix durch, usf. Die schließlich resultierende Diagonalmatrix hat dieselbe Signatur wie .

Quadriken in $\mathbb{R}^2$ .

Hermitesche Matrizen mit reellen Einträgen heißen auch symmetrisch.

Unitäre Matrizen mit reellen Einträgen heißen auch orthogonal.

Wir bemerken hier, daß eine symmetrische Matrix auch orthogonal diagonalisierbar ist, d.h. es gibt eine orthogonale Matrix so, daß $U^\mathrm{t} AU=\mathrm{E}$ .

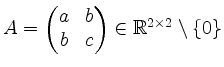Sei $A = \begin{pmatrix}a&b\\ b&c\end{pmatrix}\in\mathbb{R}^{2\times 2}\setminus\{0\}$ symmetrisch.

Seien ferner $d,\, e,\, f,\,\in\, \mathbb{R}$ beliebig. Wir betrachten die Quadrik

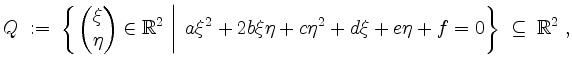
$\displaystyle Q \; := \; \left\{\left. \begin{pmatrix}\xi \\ \eta\end{pmatrix}\... ...b\xi\eta + c\eta^2 + d\xi + e\eta + f = 0\right\} \;\subseteq\;\mathbb{R}^2\;,$

definiert durch die Gleichung

$\displaystyle a\xi^2 + 2b\xi\eta + c\eta^2 + d\xi + e\eta + f \;=\; 0\;,$

welche wir vereinfachen wollen.

Das folgende Verfahren liefert die Gestalt der Quadrik ; einen Mittelpunkt oder einen Scheitelpunkt von ; eine orthogonale Matrix, deren Spalten die Hauptachsen von sind; sowie gegebenenfalls die Halbachsen von .

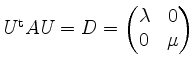Bestimme eine orthogonale Matrix $U=(u_{i,j})_{i,j}\in\mathbb{R}^{2\times 2}$ so, daß $U^\mathrm{t} AU=D=\begin{pmatrix}\lambda&0\\ 0&\mu\end{pmatrix}$ Diagonalgestalt hat. Die Spalten von stellen die Hauptachsen der Quadrik dar.
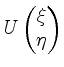Substituiert man $U\begin{pmatrix}\xi \\ \eta\end{pmatrix}$ für $\begin{pmatrix}\xi \\ \eta\end{pmatrix}$ , d.h. setzt man $u_{1,1}\xi+u_{1,2}\eta$ anstelle von $\xi$ und $u_{2,1}\xi+u_{2,2}\eta$ anstelle von $\eta$ , so wird obige Gleichung überführt in

$\displaystyle \lambda\xi^2+\mu\eta^2+d'\xi+e'\eta+f \;=\; 0$

mit $\begin{pmatrix}d' & e'\end{pmatrix}:=\begin{pmatrix}d & e\end{pmatrix}\cdot U$ .
Im Falle $\lambda\ne 0$ substituiere man $\xi+\xi_0$ für $\xi$ mit $\xi_0:=-\frac{d'}{2\lambda}$ .
Im Falle $\mu\ne 0$ substituiere man $\eta+\eta_0$ für $\eta$ mit $\eta_0:=-\frac{e'}{2\mu}$ .
Durch diese quadratische Ergänzung wird die Gleichung überführt in

$\displaystyle \lambda\xi^2+\mu\eta^2+d''\xi+e''\eta+f'' \;=\; 0$

mit gewissen $d'',e'',f''\in\mathbb{R}$ , und es gilt für $\lambda\ne 0$ , und für $\mu\ne 0$ .
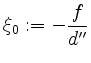Im Falle $\lambda = 0$ setze man, falls $d''\ne 0$ ist, $\xi_0:=-\dfrac{f}{d''}$ und substituiere $\xi+\xi_0$ für $\xi$ . Der konstante Term verschwindet.
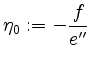Im Falle $\mu = 0$ setze man, falls $e''\ne 0$ ist, $\eta_0:=-\dfrac{f}{e''}$ und substituiere $\eta+\eta_0$ für $\eta$ . Auch hier verschwindet der konstante Term.
Durch diese linearen Substitutionen wird die Gleichung überführt in

$\displaystyle \lambda\xi^2+\mu\eta^2+d''\xi+e''\eta+f''' \;=\; 0$

mit gewissen $d'',e'',f'''\in\mathbb{R}$ .
Im Falle $f'''\ne 0$ dividiere man die Gleichung durch .
Nach eventueller Vertauschung von und ist die Gleichung nun bis auf Vorzeichen von einer der folgenden Formen.
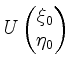- $\frac{\xi^2}{\alpha^2}+\frac{\eta^2}{\beta^2} = 1$ (Ellipse mit Mittelpunkt $U\begin{pmatrix}\xi_0 \\ \eta_0\end{pmatrix}$ und den Halbachsen $\alpha,\beta> 0$ ).
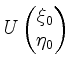- $\frac{\xi^2}{\alpha^2}-\frac{\eta^2}{\beta^2} = 1$ (Hyperbel mit Mittelpunkt $U\begin{pmatrix}\xi_0 \\ \eta_0\end{pmatrix}$ , Halbachse $\alpha>0$ und Asymptotensteigung $\dfrac{\beta}{\alpha}$ ).
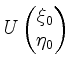- $\eta-\alpha\xi^2=0$ (nach weiterer Division durch Konstante, Parabel mit Scheitelpunkt $U\begin{pmatrix}\xi_0 \\ \eta_0\end{pmatrix}$ ).
- $\frac{\xi^2}{\alpha^2}+\frac{\eta^2}{\beta^2}=0$ (Punkt).
- $\frac{\xi^2}{\alpha^2}-\frac{\eta^2}{\beta^2}=0$ (nicht-paralleles Geradenpaar).
- $\frac{\xi^2}{\alpha^2} = 1$ (paralleles Geradenpaar).
- $\frac{\xi^2}{\alpha^2}=0$ (Gerade).
- $-\frac{\xi^2}{\alpha^2}-\frac{\eta^2}{\beta^2} = 1$ (leere Menge).
- $-\frac{\xi^2}{\alpha^2} = 1$ (leere Menge).

Zur Illustration diene die Ellipse mit der Gleichung .

$\includegraphics[width = 15cm,height = 15cm]{ellipse.eps}$

Reguläre Quadriken in $\mathbb{R}^n$ .

Sei $n\geq 1$ und sei $A\in\mathbb{R}^{n\times n}$ eine reguläre symmetrische Matrix. Sei $b\in\mathbb{R}^n$ und sei $c\in\mathbb{R}$ .

Wir betrachten die Quadrik

$\displaystyle Q \; := \; \{ x\in\mathbb{R}^n\; \vert\; x^\mathrm{t} A x + b^\mathrm{t} x + c = 0\} \;\subseteq\;\mathbb{R}^n\;,$

definiert durch die Gleichung

$\displaystyle x^\mathrm{t} A x + b^\mathrm{t} x + c \;=\; 0\;,$

welche wir vereinfachen wollen. Wegen

regulär heißt auch

regulär.

Das folgende Verfahren liefert den Mittelpunkt von ; eine orthogonale Matrix, deren Spalten die Hauptachsen von sind; die Form und gegebenenfalls die Halbachsen von .

Bestimme eine orthogonale Matrix $U\in\mathbb{R}^{n\times n}$ so, daß $U^\mathrm{t} A U = D$ Diagonalgestalt hat. Die Spalten von stellen die Hauptachsen der Quadrik dar.
Substituiert man für , so wird obige Gleichung überführt in

$\displaystyle x^\mathrm{t} D x + b'^{\mathrm{t}} x + c \;=\; 0\; ,$

wobei $b' = U^\mathrm{t} b$ .
Substituiert man nun für mit $x_0 := -\frac{1}{2} D^{-1} b'$ , so transformiert sich die beschreibende Gleichung in die Form

$\displaystyle x^\mathrm{t} D x + c' \;=\; 0\; ,$

mit $c' = x_0^\mathrm{t} D x_0 + b'^{\mathrm{t}} x_0 + c$ . Es heißt Mittelpunkt von . (Für die Existenz von $D^{-1}$ braucht man regulär.)
Ist , so ist ausgeartet. Ist $c'\neq 0$ , so dividiere man durch und erhält die Normalform

$\displaystyle x^\mathrm{t} D' x \;=\; 1\; ,$

Hat $D' = \mathrm{diag}(\delta_1,\dots,\delta_n)$ die Signatur , so heißt ein -Ellipso- -hyperboloid.
Ein -Ellipso-0 -hyperboloid heißt auch einfach Ellipsoid. Ein 0 -Ellipso- -hyperboloid ist die leere Menge.
Ist $\delta_j > 0$ , so nennt man $\delta_j^{-1/2}$ auch eine Halbachse von .
Im Falle ist ein -Ellipso-0 -hyperboloid einfach einer Ellipse, und ein -Ellipso- -hyperboloid einfach eine Hyperbel.
Im Falle spricht man statt von einem -Ellipso- -hyperboloid auch von einem einschaligen Hyperboloid und statt von einem -Ellipso- -hyperboloid auch von einem zweischaligen Hyperboloid.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele:

[Verweise]

automatisch erstellt am 22. 8. 2006