Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Folgen

Grenzwerte in Maple

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Grenzwerte können in MAPLE mit Hilfe des Befehls limit bestimmt werden. Grenzwerte für $ x \to \infty$ können dabei mit x=infinity eingegeben werden. Wird keine Richtung (mögliche Angaben: left, right, real, complex) angegeben, so wird nach Möglichkeit der beidseitige Grenzwert berechnet.

> limit ( 1/x, x=infinity);

$\displaystyle 0 $

> limit ( 1/x, x=0);

$\displaystyle \mathit{undefined} $

> limit ( arctan(1/x), x=0);

$\displaystyle \mathit{undefined} $

> limit ( 1/x, x=0, right);

$\displaystyle \infty $

> limit ( arctan(1/x), x=0, left);

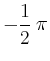
$\displaystyle - {\displaystyle \frac {1}{2}} \,\pi $


MAPLE geht bei der Berechnung davon aus, dass unbelegte Variablen reell und ungleich 0 sind. Hängt der Grenzwert vom Vorzeichen der Variable ab, so wird ggf. der Grenzwert mit der Signum-Funktion csgn angegeben bzw. bei nicht allgemein bestimmbaren Grenzwerten wird die Eingabe zurückgegeben.

> limit ( arctan(a*x), x=infinity);

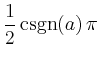
$\displaystyle {\displaystyle \frac {1}{2}} \,\mathrm{csgn}(a)\,\pi $

> limit ( exp(a*x), x=infinity);

$\displaystyle {\displaystyle \lim _{x\rightarrow \infty }} \,e^{(a\,x)} $

(Autor: Marcus Reble)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017