Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Reihen

Grenzwert einer Reihe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
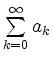Eine Summe $ \sum\limits_{k=0}^{\infty} a_k$ mit unendlich vielen Summanden bezeichnet man als Reihe. Sie konvergiert gegen einen Grenzwert

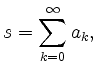
$\displaystyle s=\sum_{k=0}^\infty a_k,$

wenn die Folge $ (s_n)$ der Partialsummen

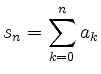
$\displaystyle s_n=\sum_{k=0}^n a_k$

gegen $ s$ konvergiert. Existiert kein Grenzwert, so bezeichnet man die Reihe als divergent.

Der Grenzwert kann von der Reihenfolge der Summanden abhängen, bzw.braucht nach dem Umordnen nicht mehr zu existieren.

Notwendig für die Konvergenz einer Reihe ist, dass

$\displaystyle \operatorname{lim} a_n = 0. $

Nur in wenigen Fällen ist die explizite Berechnung einer Reihe möglich. Ein Beispiel sind bestimmte Reihen mit rationalen Summanden wie

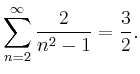
$\displaystyle \sum \limits_{n=2}^{\infty} \frac{2}{n^2-1} = \frac{3}{2}. $

Nach der Partialbruchzerlegung

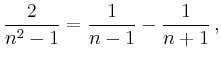
$\displaystyle \frac{2}{n^2-1} = \frac{1}{n-1} - \frac{1}{n+1}\,, $

lässt sich diese Reihe in der Form

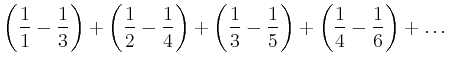
$\displaystyle \left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4... ...eft(\frac{1}{3}-\frac{1}{5}\right)+\left(\frac{1}{4}-\frac{1}{6}\right)+\hdots $

schreiben. Bis auf $ \frac{1}{1}$ und $ \frac{1}{2}$ heben sich alle Summanden auf, so dass der Grenzwert $ \frac{3}{2}$ unmittelbar abgelesen werden kann.

Für die Differenz der Partialsummen gilt für $ n < m$

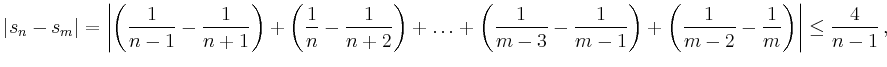
$\displaystyle \vert s_n - s_m\vert = \left\vert \left(\frac{1}{n-1} - \frac{1}{... ...) + \left(\frac{1}{m-2} - \frac{1}{m}\right)\right\vert \leq \frac{4}{n-1}\,, $

da sich die mittleren Terme aufheben. Die Partialsummen bilden also eine Cauchy-Folge:

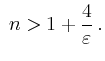
$\displaystyle \vert s_n - s_m\vert < \varepsilon \;$   für$\displaystyle \; n > 1 + \frac{4}{\varepsilon}\,. $

Die Differenz zum Grenzwert ist

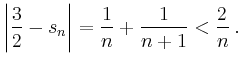
$\displaystyle \left\vert \frac{3}{2} - s_n \right\vert = \frac{1}{n} + \frac{1}{n+1} < \frac{2}{n}\,. $

Das Beispiel zeigt auch, dass die Reihenfolge der Summanden im allgemeinen wesentlich ist. Wählt man die Reihenfolge

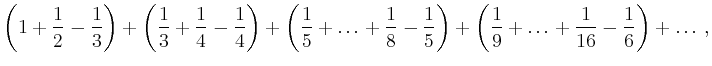
$\displaystyle \left(1 + \frac{1}{2} - \frac{1}{3}\right) + \left(\frac{1}{3} + ... ...+ \left(\frac{1}{9} + \hdots + \frac{1}{16} - \frac{1}{6}\right) + \hdots\,, $

so ist jeder Ausdruck in Klammern $ \geq \frac{1}{4}$, die Reihe also divergent.
(Autoren: Höllig/Kreitz )
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017