Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Reihen

Geometrische Reihe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
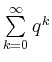Die geometrische Reihe $ \sum\limits_{k=0}^{\infty} q^k$ konvergiert genau, dann wenn $ \left\vert q \right\vert<1$.

Mit der geometrischen Summenformel

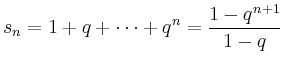
$\displaystyle s_n=1 +q +\cdots + q^n =\frac{1-q^{n+1}}{1-q} $

läßt sich der Grenzwert explizit berechnen:

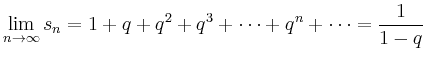
$\displaystyle \lim_{n \rightarrow \infty} s_n = 1+q +q^2 +q^3 + \cdots + q^n + \cdots = \frac{1}{1-q} $

für $ \vert q\vert<1$.

Ersetzt man ausgehend von einem gleichseitigen Dreieck rekursiv Kanten gemäß der Vorschrift

\includegraphics{koch_ersetzung.eps}

so entsteht eine Menge mit fraktalem Rand, die sogenannte Koch-Schneeflocke.

\includegraphics[width=\textwidth]{kochbilder.eps}

Die $ n$-te Schneeflocke hat $ 3\cdot 4^n$ Kanten. Da sich die Kantenlänge in jedem Schritt um einen Faktor $ 1/3$ reduziert, erhält man für den Umfang

Kantenzahl$ \ast$Kantenlänge: $ \left(3\cdot 4^{\mathit n}\right)\left(3^{\mathit{-n}}\right)=3\,\left(\frac{4}{3}\right)^{\mathit n} \rightarrow \infty\,,$
d.h.die Länge des Randes divergiert.

Im $ n$-ten Schritt werden $ 3\cdot 4^{n-1}$ gleichseitige Dreiecke mit Kantenlänge $ 3^{-n}$ und Fläche $ \sqrt{3}/4\left( 3^{-n} \right)^2$ hinzugefügt. Somit ergibt sich für den Flächeninhalt der $ n$-ten Schneeflocke


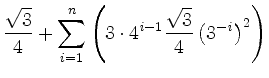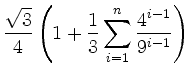$\displaystyle \frac{\sqrt{3}}{4} + \sum\limits_{i=1}^{n} \left(3\cdot 4^{\mathit i-1} \frac{\sqrt{3}}{4}\left(3^{\mathit{-i}}\right)^2\right)$ $\displaystyle =$ $\displaystyle \frac{\sqrt{3}}{4}\left(1+\frac{1}{3}\sum\limits_{i=1}^{n} \frac{4^{i-1}}{9^{i-1}}\right)$  
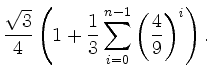  $\displaystyle =$ $\displaystyle \frac{\sqrt{3}}{4}\left(1+\frac{1}{3}\sum\limits_{i=0}^{n-1} \left(\frac{4}{9}\right)^{\mathit i} \right).$  

Die fraktale Grenzmenge hat folglich den Flächeninhalt

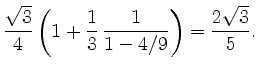
$\displaystyle \frac{\sqrt{3}}{4}\left(1+\frac{1}{3}\,\frac{1}{1-4/9}\right) = \frac{2\sqrt{3}}{5}. $

(Autoren: Höllig/Hörner)

Download:

(Dateityp: .m, 1.7K,  17.04.2008)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017