Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Konvergenz und Grenzwerte - Stetigkeit

Regeln für stetige Funktionen

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Für in einem Punkt $ a$ stetige Funktionen $ f$ und $ g$ sind
    $\displaystyle rf\quad(r\in\mathbb{R})$  
    $\displaystyle f\pm g$  
    $\displaystyle fg$  
    $\displaystyle f/g \quad($falls $\displaystyle g(a)\neq 0)$  
    $\displaystyle f\circ g$  

in $ a$ stetig.

Entsprechendes gilt für auf einem Intervall $ D$ stetige Funktion sowie für links- und rechtsseitige Stetigkeitsstellen.

Die Regeln ergeben sich unmittelbar aus den entsprechenden Aussagen für Grenzwerte. Betrachtet man beispielsweise die Komposition stetiger Funktionen, so folgt aus der Stetigkeit von $ g$ für jede Folge $ (x_n)$ mit Grenzwert $ a$

$\displaystyle \lim_{n\rightarrow\infty} g(x_n) = g(a). $

Da $ f$ ebenfalls stetig ist, folgt

$\displaystyle \lim_{n\rightarrow\infty} f(g(x_n)) = f(g(a)).$

(Autoren: App/Höllig )
Die sogenannte $ \operatorname{sinc}$-Funktion

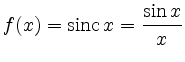
$\displaystyle f(x)=\operatorname{sinc}x=\frac{\sin x}{x}$

ist mit der Fortsetzung $ f(0)=1$ stetig auf $ \mathbb{R}$.

\includegraphics[width=.65\linewidth]{sinc_x_1.eps}

Der Beweis beruht auf Abschätzungen der trigonometrischen Funktionen.

\includegraphics[width=.3\linewidth]{sinc_1.eps}

Durch Vergleich der Flächeninhalte des Dreiecks $ \Delta (OPQ)$ , des Kreissegments und des Dreiecks $ \Delta (O\overline{P}\,\overline{Q})$ in der Abbildung sieht man, dass

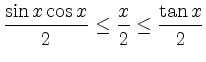
$\displaystyle \frac{\sin x \cos x }{2}\leq \frac{x}{2} \leq \frac{\tan x }{2}$

bzw.

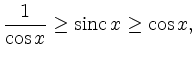
$\displaystyle \frac{1}{\cos x } \geq \operatorname{sinc} x \geq \cos x ,$

nach Division durch $ \sin x /2$ und Kehrwertbildung. Mit $ \lim\limits_{x\rightarrow 0}{\cos x }=1$ folgt aus dem Vergleichskriterium

$\displaystyle \lim_{x\rightarrow 0} \operatorname{sinc} x = 1.$

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017