Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Taylor-Entwicklung

Taylor-Polynom

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Das Taylor-Polynom

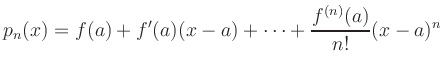
$\displaystyle p_n(x) = f(a) + f'(a) (x-a) + \cdots + \frac{f^{(n)}(a)}{n!} (x-a)^n $

interpoliert die Ableitungen einer Funktion $ f$ im Punkt $ a$ bis zur Ordnung $ n$, d. h. $ p_n^{(k)}(a)=f^{(k)}(a)\,,\; k= 0,\ldots ,n$. Ist $ f$ $ (n+1)$-mal stetig differenzierbar, so gilt

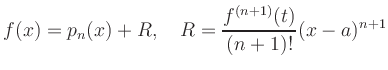
$\displaystyle f(x) = p_n(x) + R,\quad R = \frac{f^{(n+1)}(t)}{(n+1)!} (x-a)^{n+1} $

für ein $ t$ zwischen $ a$ und $ x$.

Direktes Nachrechnen zeigt die Übereinstimmung der Ableitungen von $ f$ und $ p_n$.

Zur Überprüfung des Restglieds $ R$ ergänzt man das Taylor-Polynom um einen weiteren Term:

$\displaystyle q(y) = p_n(y) + c (y-a)^{n+1}\,. $

Die Konstante $ c$ ist so gewählt, dass $ q(x)=f(x)$. Folglich hat $ q-f$ eine Nullstelle mit Vielfachheit $ n+1$ bei $ y=a$ und eine weitere Nullstelle bei $ y=x$, ingesamt also $ n+2$ Nullstellen. Nach dem Satz von Rolle muß die $ (n+1)$-te Ableitung mindestens eine Nullstelle $ t$ haben:

$\displaystyle 0 = q^{(n+1)}(t) - f^{(n+1)}(t) = c (n+1)! - f^{(n+1)}(t)\, . $

Aus

$\displaystyle R = f(x) - p_n(x) = q(x) - p_n(x) = c (x-a)^{n+1} $

ergibt sich die behauptete Form des Restglieds.

Die Ableitungen der Sinusfunktion $ f(x) = \sin{x}$ sind

$\displaystyle f^{'} = \cos{x},\quad f^{''} = -\sin{x},\quad f^{'''} = -\cos{x},\quad f^{4} = f = \sin{x}, ... \,. $

Mit den Werten

$\displaystyle f^{'}(0) = 1,\quad f^{''}(0) = 0,\quad f^{'''}(0) = -1,\quad f^{4}(0) = f = 0, ... \,. $

sind die ersten Taylor-Polynome der Sinusfunktion

$\displaystyle p_1(x)$ $\displaystyle = x$    
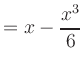$\displaystyle p_3(x)$ $\displaystyle = x -\frac{x^3}{6}$    
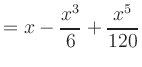$\displaystyle p_5(x)$ $\displaystyle = x -\frac{x^3}{6} + \frac{x^5}{120}$    
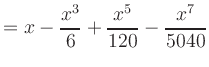$\displaystyle p_7(x)$ $\displaystyle = x -\frac{x^3}{6} + \frac{x^5}{120} - \frac{x^7}{5040}$    

Entsprechend gilt für die Kosinusfunktion

$\displaystyle p_0(x)$ $\displaystyle = 1$    
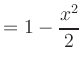$\displaystyle p_2(x)$ $\displaystyle = 1 - \frac{x^2}{2}$    
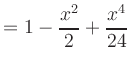$\displaystyle p_4(x)$ $\displaystyle = 1 - \frac{x^2}{2} + \frac{x^4}{24}$    
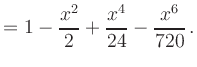$\displaystyle p_6(x)$ $\displaystyle = 1 - \frac{x^2}{2} + \frac{x^4}{24} - \frac{x^6}{720}\,.$    

Die Approximation ist für kleine $ x$ sehr genau. Beispielsweise kann der Fehler der Näherung

$\displaystyle \sin{0.1} \approx p_{4}(0.1) = 0.09983... $

durch

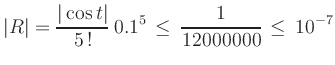
$\displaystyle \vert R\vert = \frac{\vert\cos{t}\vert}{5\,!}\,0.1^5 \, \leq \, \frac{1}{12000000} \, \leq \, 10^{-7} $

abgeschätzt werden.
\includegraphics[height=4.5cm]{Taylor_sin}   \includegraphics[height=4.5cm]{Taylor_cos}

Wie aus der Abbildung ersichtlich ist, wird die Approximation für großes $ x$ erst bei höheren Graden hinreichend genau. In der Tabelle sind die Fehler für einige $ x$-Werte angegeben.

$ x$ $ \pi$ $ \pi/2$ $ \pi/3$ $ \pi/4$ $ \pi/5$ $ \pi/6$
$ p_1(x)$ 3.1416 0.5708 0.1812 0.0783 0.0405 0.0236
$ p_3(x)$ 2.0261 0.0752 0.0102 0.0025 0.0008 0.0003
$ p_5(x)$ 0.5240 0.0045 0.0003 0.0000 0.0000 0.0000
$ p_7(x)$ 0.0752 0.0002 0.0000 0.0000 0.0000 0.0000
$ p_0(x)$ 2.0000 1.0000 0.5000 0.2929 0.1910 0.1340
$ p_2(x)$ 2.9348 0.2337 0.0483 0.0155 0.0064 0.0031
$ p_4(x)$ 1.1239 0.0200 0.0018 0.0003 0.0001 0.0000
$ p_6(x)$ 0.2114 0.0009 0.0000 0.0000 0.0000 0.0000
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017