Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Analysis einer Veränderlichen - Differentiation - Taylor-Entwicklung

Reelle Taylor-Reihe

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Taylor-Reihe einer unendlich oft differenzierbaren Funktion $ f$ im Punkt $ x_0$ ist eine Entwicklung in eine Potenz-Reihe:

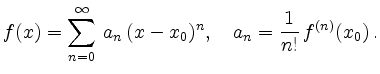
$\displaystyle f(x) = \sum_{n=0}^\infty\,a_n\,(x-x_0)^n,\quad a_n = \frac{1}{n!}\,f^{(n)}(x_0)\,. $

Für $ x \in \mathbb{R}$ konvergiert die Reihe sowie alle ihre Ableitungen absolut in einem Intervall $ (x_0-r, x_0+r)$ und divergiert für $ \vert x - x_0\vert > r$ . Für $ \vert x - x_0\vert = r$ sind ohne weitere Untersuchungen keine Aussagen über die Konvergenz der Reihe möglich.

Die Schranke $ r$ für den Abstand vom Entwicklungspunkt wird als Konvergenz-Radius bezeichnet und lässt sich mit der Formel

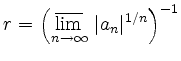
$\displaystyle r = \left( \operatorname*{\overline{\lim}}_{n\to\infty}\,\vert a_n\vert^{1/n} \right)^{-1} $

berechnen. Dabei sind die Werte $ r=0$ und $ r=\infty$ möglich. Das Konvergenz-Intervall ist in diesen Fällen leer bzw. ganz $ \mathbb{R}$ .

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)

(Inhalt vorübergehend nicht verfügbar)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 5.1.2017