Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Analytische Geometrie - Quadriken

Hauptachsentransformation

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Durch eine Drehung und Verschiebung kann eine Quadrik im $ \mathbb{R}^n$ auf Normalform transformiert werden:

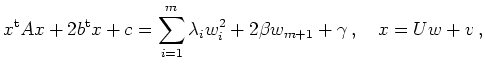
$\displaystyle x^{\operatorname t}A x + 2 b^{\operatorname t}x + c = \sum_{i=1}^m \lambda_i w_i^2 + 2\beta w_{m+1} + \gamma \,, \quad x=Uw+v \,, $

wobei $ m = \operatorname{Rang}A$ und $ \beta\gamma=0$ gilt.

\includegraphics[width=\moimagesize]{a_hauptachsentrafo}

Dabei enthalten die Spalten der Drehmatrix $ U$ die Eigenvektoren $ u_i$ zu den Eigenwerten $ \lambda_i$ von $ A$, deren Richtungen als Hauptachsen bezeichnet werden. Der Verschiebungsvektor $ v$ ist der Mittelpunkt der Quadrik.

(Inhalt vorübergehend nicht verfügbar)
Die Quadrik

$\displaystyle Q:\quad 8x_1^2 + 17x_2^2 + 20x_3^2 + 20x_1x_2 + 8x_1x_3 + 28x_2x_3 - 48x_1 - 114x_2 - 78x_3 + 207 =0 $

soll auf Normalform transformiert werden.

In Matrixschreibweise ergibt sich

$\displaystyle Q:\quad x^{\operatorname t}A x + 2b^{\operatorname t}x + c =0 $

mit

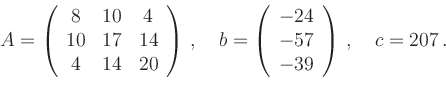
\begin{displaymath} A=\left( \begin{array}{ccc} 8 & 10 & 4\\ 10 & 17 & 14\\ 4 ... ...ray}{c} -24 \\ -57 \\ -39 \end{array} \right)\,,\quad c=207\,. \end{displaymath}

Die Matrix $ A$ hat die Eigenwerte $ 9$, $ 36$ und 0, zugehörige normierte Eigenvektoren $ u_i$ mit $ \operatorname{det}(u_1,u_2,u_3) = 1$ sind z.B.

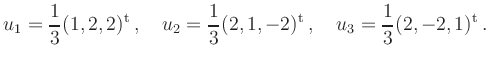
$\displaystyle u_1=\frac{1}{3}(1,2,2)^{\operatorname t}\,,\quad u_2=\frac{1}{3}(2,1,-2)^{\operatorname t}\,,\quad u_3=\frac{1}{3}(2,-2,1)^{\operatorname t}\,. $

Nach der Transformation $ x=Uy$ mit $ U=(u_1,u_2,u_3)$ erhält man

$\displaystyle Q:\quad 36y_1^2 + 9 y_2^2 - 144y_1 - 18y_2 + 18y_3 + 207 = 0\,. $

Durch die quadratische Ergänzung $ z_1=y_1-2$, $ z_2=y_2-1$, $ z_3=y_3$ ergibt sich

$\displaystyle Q:\quad 36z_1^2 + 9z_2^2 + 18z_3 + 54 = 0\,. $

Skalierung (Division durch 9) und die Verschiebung $ \xi_1=z_1$, $ \xi_2=z_2$, $ \xi_3=z_3+3$ liefert schließlich die Normalform

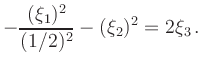
$\displaystyle Q:\quad 4\xi_1^2 + \xi_2^2 + 2\xi_3 =0\,$   bzw.$\displaystyle -\frac{(\xi_1)^2}{(1/2)^2}-(\xi_2)^2 = 2 \xi_3 \,. $

Die Quadrik ist also ein elliptisches Paraboloid mit Halbachsenlängen $ 1/2$ und $ 1$.

Insgesamt hat die Transformation die Form

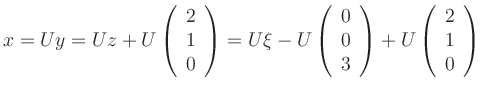
$\displaystyle x = Uy = Uz + U \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array... ...d{array} \right) + U \left(\begin{array}{c} 2 \\ 1 \\ 0 \end{array} \right) $

Die Verschiebung ist

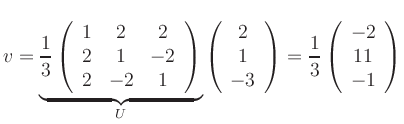
$\displaystyle v = \underbrace{ \frac{1}{3}\left(\begin{array}{ccc} 1 & 2 & 2 \\... ...ht) = \frac{1}{3}\left( \begin{array}{c} -2 \\ 11 \\ -1 \end{array} \right) $

und entspricht dem Mittelpunkt der Quadrik.

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012