Mathematik-Online-Kurs: Lineare Algebra-Analytische Geometrie-Quadriken-Kegelschnitt

	[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
	Mathematik-Online-Kurs: Lineare Algebra - Analytische Geometrie - Quadriken
	Kegelschnitt

Der Schnitt eines Doppel-Kegels

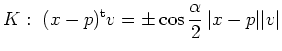
$\displaystyle K:\ (x-p)^{\operatorname t}v = \pm\cos{\frac{\alpha}{2}} \,\vert x-p\vert\vert v\vert$

mit Spitze

( $p_3\ne 0$ ), Richtung

und Öffnungswinkel $\alpha$ mit der Ebene $E:\ x_3=0$ ist eine quadratische Kurve

$\displaystyle K\cap E:\ a_{1,1} x_1^2 + 2a_{1,2} x_1x_2 + a_{2,2} x_2^2 + 2b_1 x_1 + 2b_2 x_2 + c = 0\,.$

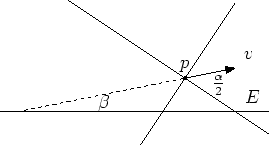
$\includegraphics{b_kegelschnitt_skizze}$

Der Typ des Kegelschnitts hängt von der Größe des Winkels $\beta$ zwischen und der Geraden , $t\in\mathbb{R}$ , ab.

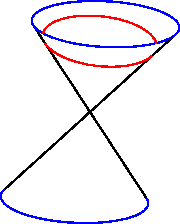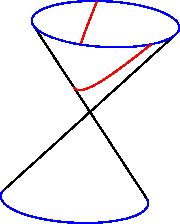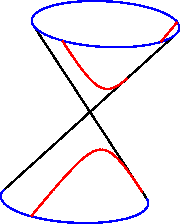$\includegraphics{a_kegelschnitt_1}$	$\includegraphics{a_kegelschnitt_2}$	$\includegraphics{a_kegelschnitt_3}$
Ellipse: $\beta>\alpha/2$	Parabel: $\beta=\alpha/2$	Hyperbel: $\beta<\alpha/2$

automatisch erstellt am 14.6.2012