Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Matrizen - Lineare Abbildungen

Matrix

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Unter einer $ (m\times n)$-Matrix ( $ m,n \in \mathbb{N}$) über einem Körper $ K$ versteht man ein Rechteckschema

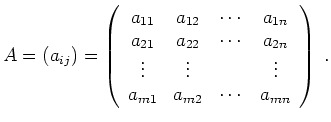
$\displaystyle A = (a_{ij}) = \left( \begin{array}{ccccc} a_{11} & a_{12} & \cdo... ...ts & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) \; . $

Man bezeichnet $ (a_{i1},a_{i2},\dots,a_{in})$ als $ i$-ten Zeilen- und $ (a_{1j},a_{2j},\dots,a_{mj})^{\operatorname t}$ als $ j$-ten Spaltenvektor von $ A$. Speziell ist eine $ (n \times 1)$-Matrix ein Spalten- und eine $ (1 \times n)$-Matrix ein Zeilenvektor.

Die Gesamtheit aller $ (n\times m)$-Matrizen wird mit $ K^{n \times m}$ bezeichnet; $ \mathbb{R}^{n\times m}$ ( $ \mathbb{C}^{n\times m}$) bezeichnet die reellen (komplexen) Matrizen.

Die folgenden Beispiele illustrieren verschiedene Matrixdimensionen.

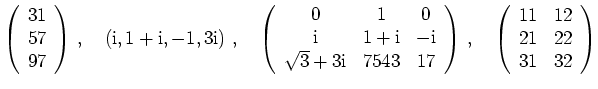
$\displaystyle \left( \begin{array}{c} 31\\ 57\\ 97\end{array}\right)\,,\quad \l... ...left( \begin{array}{ccccc} 11 & 12 \\ 21 & 22 \\ 31 & 32 \end{array}\right) $

Die ersten beiden Matrizen sind Spalten- bzw. Zeilenvektoren, d.h. Matrizen, bei denen eine der Dimensionen $ 1$ ist. Rechts ist eine quadratische und eine rechteckige Matrix gezeigt.

(Autoren: Höllig/Hörner)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012