Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Lineare Gleichungssysteme - Klassifikation und allgemeine Struktur

Lineares Gleichungssystem

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ein lineares Gleichungssystem über einem Körper $ K$ hat die Form

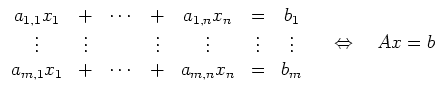
$\displaystyle \begin{array}{ccccccc} a_{1,1}x_1 & + & \cdots & + & a_{1,n}x_n ... ... & + & a_{m,n}x_n & = & b_m \end{array} \quad \Leftrightarrow \quad Ax = b $

mit einer Koeffizientenmatrix $ A = (a_{i,j})\in K^{m\times n}$, zu bestimmenden Unbekannten $ x_j \in K$ und einer rechten Seite $ b\in K^m$.

Das lineare Gleichungssystem nennt man homogen, wenn $ b = 0$, sonst bezeichnet man es als inhomogen.

Für ein reelles ( $ K=\mathbb{R}$) oder komplexes ( $ K=\mathbb{C}$) lineares Gleichungssystem wird $ K$ nicht explizit angegeben. Welcher Fall vorliegt, ist meist aus dem Zusammenhang ersichtlich.

Besitzt das Lineare Gleichungssystem keine Lösung (im Allgemeinen für $ m>n$), so bezeichnet man es als überbestimmt. Man spricht in diesem Fall auch von einem Ausgleichsproblem. Ein Lineares Gleichungssystem mit keiner eindeutigen Lösung (im Allgemeinen für $ m<n$) nennt man unterbestimmt.

Eine Funktion $ f(x)$ kann aus Daten

$\displaystyle (x_i,f_i),\quad i=1,\ldots,n\, , $

durch Interpolation näherungsweise rekonstruiert werden. Verwendet man einen linearen Ansatz

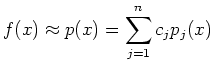
$\displaystyle f(x) \approx p(x) = \sum_{j=1}^n c_j p_j(x) $

mit geeigneten Basisfunktionen $ p_j$, so ergibt sich aus den Interpolationsbedingungen

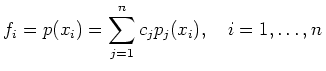
$\displaystyle f_i = p(x_i) = \sum_{j=1}^n c_j p_j(x_i),\quad i=1,\ldots,n\, $

das lineare Gleichungssystem für die $ c_j$ als

$\displaystyle Ac=b\,, $

mit $ a_{i,j}=p_j(x_i)$ und $ b_i=f_i$.

\includegraphics[width=.6\linewidth]{b_interpolation}

In dem abgebildeten Beispiel einer Tour-de-France-Etappe ist mit jedem Datenpunkt eine Exponentialfunktion

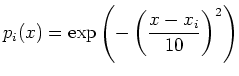
$\displaystyle p_i(x) = \exp\left(-\left(\frac{x-x_i}{10}\right)^2\right) $

assoziiert. Durch das starke Abklingen von $ p_i$ für $ \vert x-x_i\vert\to\infty$ wird erreicht, dass sich bei der Interpolation Änderungen in Datenpunkten vorwiegend lokal auswirken.
(Autoren: App/Höllig)
Bezeichnet man in einem elektrischen Schaltkreis mit $ x_i$ die Kreisströme mit Fließrichtung entgegen dem Uhrzeigersinn, mit $ R_{i,j}$ den gemeinsamen Widerstand der $ i$-ten und $ j$-ten Schleife und mit $ U_i$ die angelegten Spannungen, so ergibt sich aus dem Ohmschen und dem Kirchhoffschen Gesetz das lineare Gleichungssystem

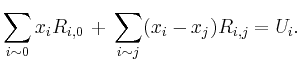
$\displaystyle \sum_{i\sim 0} x_i R_{i,0}\, +\, \sum_{i\sim j} (x_i-x_j)R_{i,j} = U_i. $

Dabei bedeutet $ i\sim j$, dass die $ i$-te und $ j$-te Schleife einen gemeinsamen Widerstand haben. $ x_i-x_j$ ist der Strom durch diesen Widerstand. Mit $ R_{i,0}$, $ i\sim 0$, werden Widerstände bezeichnet, die nur in der $ i$-ten Schleife liegen.

\includegraphics[width=\moimagesize]{b_elektrischer_schaltkreis}

Beispielsweise erhält man für den abgebildeten Schaltkreis das lineare Gleichungssystem

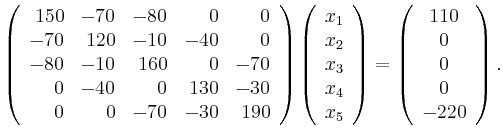
$\displaystyle \left(\begin{array}{rrrrr} 150 & -70 & -80 & 0 & 0 \\ -70 & 120 ... ...right) = \left(\begin{array}{c} 110 \\ 0 \\ 0 \\ 0 \\ -220 \end{array}\right). $

Die Koeffizientenmatrix enthält in der Diagonale jeweils die Summe der zu einer Schleife gehörigen Widerstände und in Position $ (i,j)$ den negativen gemeinsamen Widerstand der Schleifen $ i$ und $ j$. Die Lösung für das betrachtete Beispiel ist

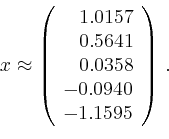
\begin{displaymath} x \approx \left( \begin{array}{r} 1.0157\\ 0.5641\\ 0.0358\\ -0.0940\\ -1.1595 \end{array}\right)\,. \end{displaymath}

(Autoren: App/Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012