Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Lineare Gleichungssysteme - Klassifikation und allgemeine Struktur

Lösbarkeit eines linearen Gleichungssystems

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Die Lösungsmenge eines homogenen linearen Gleichungssystems über einem Körper $ K$ ,

$\displaystyle Ax = 0, $

mit einer $ m\times n$ Koeffizientenmatrix $ A$ ist ein Unterraum $ U$ von $ K^n$ .

Besitzt das inhomogene lineare Gleichungssystem

$\displaystyle Ax = b $

eine Lösung $ v$ , so gilt für die allgemeine Lösung

$\displaystyle x \in v + U\, , $

d.h. die Lösungsmenge ist ein affiner Unterraum von $ K^n$ . Insbesondere kann also ein inhomogenes lineares Gleichungssystem entweder keine, eine ($ U=\{0\}$ ) oder unendlich viele ( $ \operatorname{dim} U>0$ ) Lösungen besitzen.
Sind $ x,y$ Lösungen des homogenen linearen Gleichungssystems und $ \lambda\in K$, so erhält man

$\displaystyle A(x+y)$ $\displaystyle = Ax + Ay = 0 + 0 = 0$    

sowie


$\displaystyle A(\lambda x)$ $\displaystyle = \lambda Ax = \lambda 0 = 0\,,$    

d.h. die Lösungsmenge des homogenen linearen Gleichungssystems bildet einen Unterraum $ U$.

Falls $ v$ eine Lösung des inhomogenen linearen Gleichungssystems ist und $ u\in U$, so ist $ x=v+u$ wegen

$\displaystyle Ax = A(v+u) = Av +Au = b+0 =b $

ebenfalls eine Lösung des inhomogenen linearen Gleichungssystems. Umgekehrt ist mit zwei Lösungen $ v$ und $ w$ des inhomogenen linearen Gleichungssystems die Differenz $ v-w$ wegen

$\displaystyle A(v-w) = Av -Aw =b -b =0 $

eine Lösung des homogenen linearen Gleichungssystems.

Man erhält somit alle Lösungen eines inhomogenen linearen Gleichungssystems, indem man für eine beliebige Lösung des inhomogenen linearen Gleichungssystems die Summen mit allen Lösungen des homogenen linearen Gleichungssystems bildet.

(Autoren: App/Höllig)
Die folgenden einfachen Fälle veranschaulichen die verschiedenen Typen von linearen Gleichungssystemen:

(i) Das lineare Gleichungssystem

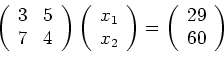
\begin{displaymath} \left( \begin{array}{cc} 3 & 5 \\ 7 & 4 \end{array}\right) ... ...}\right) = \left( \begin{array}{c} 29\\ 60 \end{array}\right) \end{displaymath}

besitzt die eindeutige Lösung $ x_1=8$, $ x_2=1$.

(ii) Das lineare Gleichungssystem

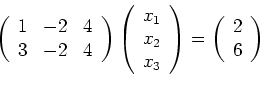
\begin{displaymath} \left( \begin{array}{ccc} 1 & -2 & 4 \\ 3 & -2 & 4 \end{arr... ...ay}\right) = \left( \begin{array}{c} 2\\ 6 \end{array}\right) \end{displaymath}

besitzt keine eindeutige Lösung. Wählt man $ x_3=t$ beliebig, so erhält man $ x_2=2t$, $ x_1=2$ als Lösung.

(iii) Das lineare Gleichungssystem

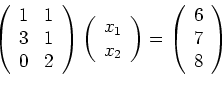
\begin{displaymath} \left( \begin{array}{cc} 1 & 1 \\ 3 & 1 \\ 0 & 2 \end{arra... ...ight) = \left( \begin{array}{c} 6\\ 7\\ 8 \end{array}\right) \end{displaymath}

besitzt keine Lösung. Die letzte Zeile liefert $ x_2=4$, setzt man dies aber in die anderen Zeilen ein, so erhält man aus der ersten Zeile $ x_1=2$, aus der zweiten hingegen $ x_1=1$.
(Autoren: App/Höllig)
[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012