Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] Englische Flagge
Mathematik-Online-Kurs: Lineare Algebra - Normalformen - Jordan-Normalform

Hauptvektoren

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
Ist $ \lambda$ ein Eigenwert der komplexen $ (n \times n)$-Matrix $ A$ mit algebraischer Vielfachheit $ m$ so nennt man einen Vektor $ v$ mit

$\displaystyle (A-\lambda E)^mv=0\,,\quad v\neq 0 $

Hauptvektor zum Eigenwert $ \lambda$.

Alle Hauptvektoren zu einem Eigenwert bilden zusammen mit dem Nullvektor einen Untervektorraum der Dimension $ m$, den Hauptraum $ H_\lambda$ zum Eigenwert $ \lambda$. Dieser ist invariant unter der linearen Abbildung $ A$.

Der Gesamtraum ist die direkte Summe der Haupträume:

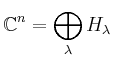
$\displaystyle \mathbb{C}^n = \bigoplus_{\lambda} H_{\lambda} $

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 14.6.2012