Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis

Kurvenintegrale und konservative Vektorfelder

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Kurven.

Sei $ n\ge 1$ . Eine Kurve im $ \mathbb{R}^n$ ist eine stetige Abbildung $ \gamma:[a,b]\to\mathbb{R}^n$ für gewisse $ a,\,b\in\mathbb{R}$ mit $ a < b$ . Man nennt $ \gamma(a)$ den Anfangspunkt und $ \gamma(b)$ den Endpunkt der Kurve $ \gamma$ . Eine Kurve, deren Anfangspunkt gleich ihrem Endpunkt ist, heißt geschlossene Kurve.

Der Träger einer Kurve $ \gamma$ ist definiert als

$\displaystyle \mathcal T(\gamma) \; :=\; \left\{\gamma(t)\; \vert \; t\in [a,b]\right\}. $

Falls $ \mathcal T(\gamma)\subseteq G$ für eine offene Teilmenge $ G\subseteq\mathbb{R}^n$ , so nennt man $ \gamma$ eine Kurve in $ G$ .

Ist die Funktion $ \gamma=(\gamma_1,\dots,\gamma_n)^\mathrm{t}$ differenzierbar, so heißt

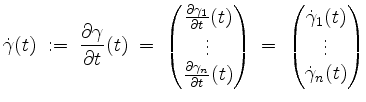
$\displaystyle \dot{\gamma}(t) \; :=\; \frac{\partial \gamma}{\partial t}(t) \; ... ...=\; \begin{pmatrix}\dot{\gamma}_1(t)\\ \vdots\\ \dot{\gamma}_n(t)\end{pmatrix}$

der Tangentialvektor von $ \gamma$ an der Stelle $ t$ . In den Randpunkten $ a$ bzw. $ b$ ist dabei die rechtsseitige bzw. linksseitige Ableitung zu betrachten.

Die Kurve $ \gamma$ heißt stückweise stetig differenzierbar, falls es so eine Unterteilung $ a=x_0<x_1<\dots<x_m=b$ gibt, daß $ \gamma \vert _{[x_{k-1},x_k]}$ stetig differenzierbar ist für $ k=1,\dots,m$ . Eine stückweise stetig differenzierbare Kurve nennt man auch Weg.

Die Länge eines solchen Weges $ \gamma:[a,b]\to\mathbb{R}^n$ ist gegeben durch

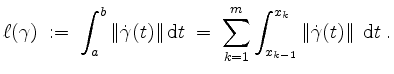
$\displaystyle \ell(\gamma)\; :=\; \int_a^b\left\Vert\dot{\gamma}(t)\right\Vert\... ...1}^m \int_{x_{k-1}}^{x_k}\left\Vert\dot{\gamma}(t)\right\Vert\;\mathrm{d}t\; . $

Kurvenintegrale.

Sei $ \gamma:[a,b]\to\mathbb{R}^n$ ein Weg und $ f:\mathcal T(\gamma)\to\mathbb{R}^n$ eine stetige Funktion. Dann ist das Kurvenintegral von $ f$ längs $ \gamma$ gegeben durch

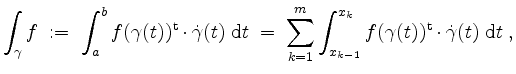
$\displaystyle \int_\gamma f\; :=\;\int_a^b f(\gamma(t))^\mathrm{t}\cdot \dot{\g... ...t_{x_{k-1}}^{x_k}f(\gamma(t))^\mathrm{t}\cdot \dot{\gamma}(t)\;\mathrm{d}t\; , $

wobei $ a=x_0<x_1<\dots<x_m=b$ so eine Unterteilung sei, daß $ \gamma \vert _{[x_{k-1},x_k]}$ stetig differenzierbar ist für $ k\in\{1,\dots,m\}$ .

Schreibt man $ f=(f_1,\ldots,f_n)^\mathrm{t}$ und $ \gamma=(\gamma_1,\ldots,\gamma_n)^\mathrm{t}$ , so sei auch folgende Schreibweise erlaubt.

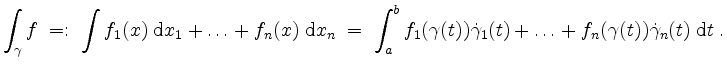
$\displaystyle \int_\gamma f \;=:\; \int f_1(x)\;\mathrm{d}x_1+\ldots+f_n(x)\;\... ...ma(t))\dot{\gamma}_1(t)+\ldots+f_n(\gamma(t))\dot{\gamma}_n(t)\;\mathrm{d}t\;. $

Zum Beispiel sei $ n:=2$ , $ f:\mathbb{R}^2\to\mathbb{R}^2$ , $ f(x,y):=(-y,x)^\mathrm{t}$ , und $ \gamma:[a,b]\to\mathbb{R}^2$ ein Weg. Dann kann man schreiben

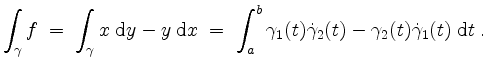
$\displaystyle \int_\gamma f \;=\; \int_\gamma x\;\mathrm{d}y-y\;\mathrm{d}x \;... ..._a^b \gamma_1(t)\dot{\gamma}_2(t)-\gamma_2(t)\dot{\gamma}_1(t)\;\mathrm{d}t\;. $

Äquivalenz von Kurven.

Zwei Wege $ \gamma:[a,b]\to\mathbb{R}^n$ und $ \delta:[c,d]\to\mathbb{R}^n$ heißen äquivalent, falls es eine bijektive, streng monoton wachsende Funktion $ \varphi:[a,b]\to [c,d]$ so gibt, daß $ \gamma=\delta\circ\varphi$ . D.h. es ist $ \gamma(t) = \delta(\varphi(t))$ für alle $ t\in [a,b]$ .

Sind $ \gamma$ und $ \delta$ äquivalente Wege im $ \mathbb{R}^n$ , so sind

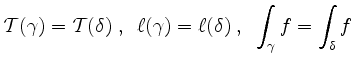
$\displaystyle \mathcal T(\gamma)=\mathcal T(\delta)\;,\;\; \ell(\gamma)=\ell(\delta)\;,\;\; \int_\gamma f=\int_\delta f $

für alle stetigen Funktionen $ f:\mathcal T(\gamma)\to\mathbb{R}^n$ .

Grob gesagt, die Länge eines Weges und das Kurvenintegral längs eines Weges hängt nur vom Träger der Kurve und dem Durchlaufsinn ab. Daher kann man eine Kurve auch als Menge im $ \mathbb{R}^n$ zusammen mit einem Durchlaufsinn betrachten. Eine zugehörige Abbildung $ \gamma:[a,b]\to\mathbb{R}^n$ heißt dann eine Parameterdarstellung der Kurve, und alle möglichen Parameterdarstellungen sind zueinander äquivalent.

Einfacher Zusammenhang und Sterngebiete.

Sei $ G\subseteq\mathbb{R}^n$ ein Gebiet, d.h. eine offene und zusammenhängende Teilmenge.

Das Gebiet $ G$ heißt einfach zusammenhängend, falls sich jeder geschlossene Weg $ \gamma: [a,b]\to G$ stetig in einen Punkt zusammenziehen läßt, ohne $ G$ zu verlassen. Formal besagt diese Forderung, es gebe für jedes solche $ \gamma$ eine stetige Funktion $ H:[a,b]\times [0,1]\longrightarrow G$ mit $ H\circ\iota_0 = \gamma$ und $ H\circ\iota_1$ konstant, wobei $ \iota_s : [a,b] \longrightarrow [a,b]\times [0,1]$ , $ t\mapsto (t,s)$ .

Ein Gebiet $ G\subseteq\mathbb{R}^2$ in der Ebene ist einfach zusammenhängend genau dann, wenn es, anschaulich gesprochen, ,,keine Löcher hat``.

Zum Beispiel ist die punktierte Ebene $ \mathbb{R}^2\setminus\{(0,0)^\mathrm{t}\}$ nicht einfach zusammenhängend.

Dieses anschauliche Kriterium läßt sich nicht direkt auf mehr Dimensionen verallgemeinern. Zum Beispiel ist der punktierte Raum $ \mathbb{R}^3\setminus\{0\}$ einfach zusammenhängend.

Ein Gebiet $ G\subseteq\mathbb{R}^n$ heißt sternförmig, falls es ein Zentrum $ z\in G$ gibt so, daß für alle $ x\in G$ die Verbindungsstrecke $ \overline{x,z}$ in $ G$ enthalten ist.

Zum Beispiel ist jedes konvexe Gebiet sternförmig. Andererseits ist ist die geschlitzte Ebene $ \mathbb{R}^2\setminus (\mathbb{R}_{<0}\times\{0\})$ sternförmig mit Zentrum $ z = (1,0)^\mathrm{t}$ , aber nicht konvex.

Jedes sternförmige Gebiet ist einfach zusammenhängend.

Andererseits ist die Menge

$\displaystyle \{(\xi_1,\xi_2)^\mathrm{t}\in\mathbb{R}^2\vert\; 4<\xi_1^2+\xi_2^2<9,\; \xi_2>0\} $

einfach zusammenhängend, aber nicht sternförmig, wie man der Skizze entnimmt.
\includegraphics[width = 8cm]{r.eps}

Konservative Vektorfelder.

Sei $ G\subseteq\mathbb{R}^n$ ein Gebiet. Sei $ f=(f_1,\ldots,f_n)^\mathrm{t}:G\to\mathbb{R}^n$ eine Funktion. Man nennt $ f$ dann auch ein Vektorfeld.

Eine Stammfunktion von $ f$ ist eine differenzierbare Funktion $ F:G\to\mathbb{R}$ so, daß $ \nabla F=f$ , d.h. $ F'=f^\mathrm{t}$ . Falls eine Stammfunktion $ F$ von $ f$ existiert, so spricht man bei $ f$ auch von einem konservativen Vektorfeld (oder einem Gradientenfeld).

Für ein Vektorfeld $ f:G\to\mathbb{R}^n$ sind folgende Aussagen äquivalent:

Die zweite Eigenschaft bezeichnet man auch als die Wegunabhängigkeit des Kurvenintegrals längs $ f$ .

Der erste Hauptsatz für Kurvenintegrale besagt folgendes. Ist das Vektorfeld $ f:G\to\mathbb{R}^n$ konservativ, und ist $ F:G\to\mathbb{R}$ eine Stammfunktion von $ f$ , so gilt für jeden Weg $ \gamma: [a,b]\to G$

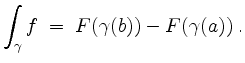
$\displaystyle \int_\gamma f \;=\; F(\gamma(b))-F(\gamma(a))\;. $

Ist $ \gamma$ ein geschlossener Weg und $ f$ ein konservatives Vektorfeld, so gilt also $ \int_\gamma f=0$ .

Integrabilitätsbedingungen.

Sei $ G\subseteq\mathbb{R}^n$ ein Gebiet. Sei $ f=(f_1,\ldots,f_n)^\mathrm{t}:G\to\mathbb{R}^n$ ein Vektorfeld.

Wir sagen, $ f$ erfüllt die Integrabilitätsbedingungen, falls $ f$ stetig differenzierbar ist und

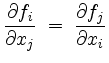
$\displaystyle \frac{\partial f_i}{\partial x_j} \;=\; \frac{\partial f_j}{\partial x_i} $

auf $ G$ erfüllt für alle $ i,j\in\{1,\ldots,n\}$ .

Ein stetig differenzierbares konservatives Vektorfeld erfüllt stets die Integrabilitätsbedingungen, wie man mit Hilfe des Satzes von Schwarz sieht.

Der zweite Hauptsatz für Kurvenintegrale besagt folgendes. Ist $ f:G\to\mathbb{R}^n$ ein stetig differenzierbares Vektorfeld auf einem einfach zusammenhängenden Gebiet $ G$ , so ist $ f$ konservativ genau dann, wenn $ f$ die Integrabilitätsbedingungen erfüllt.

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele

Aufgaben

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 16.2.2011