
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis

|
[Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen] |
|
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis | |
Das mehrdimensionale Riemann-Integral |
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
Integration über Quader.
Es seien ![]() und
und
![]() mit
mit ![]() für alle
für alle
![]() .
Es ist
.
Es ist
![]() ein n-dimensionaler Quader. Dessen Volumen
ist definiert als
ein n-dimensionaler Quader. Dessen Volumen
ist definiert als
Sei für alle
![]() eine Unterteilung
eine Unterteilung
![]() von
von ![]() gewählt. Dann heißt das kartesische Produkt
gewählt. Dann heißt das kartesische Produkt
eine Unterteilung des Quaders
Zum Beispiel ist
![]() eine Unterteilung des Quaders
eine Unterteilung des Quaders
![]() .
.
Für jedes Tupel
![]() mit
mit
![]() für
für
![]() heißt
heißt
![$\displaystyle I_{\underline{x},\underline{\nu}} \; :=\; \left[x_{\nu_1-1}^{(1)}...
...)}\right] \times \dots \times
\left[x_{\nu_n-1}^{(n)}, x_{\nu_n}^{(n)}\right]
$](/inhalt/vstatisch/vstatisch62/img15.png)
ein Teilquader von
Sei
![]() eine beschränkte Funktion.
eine beschränkte Funktion.
Das Volumen zwischen der
![]() -Ebene und dem Funktionsgraphen wird von oben angenähert durch die
Obersumme
-Ebene und dem Funktionsgraphen wird von oben angenähert durch die
Obersumme
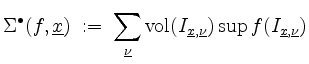
und von unten durch die Untersumme
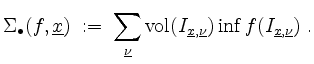
Dabei erstrecken sich die Summen über alle möglichen Tupel
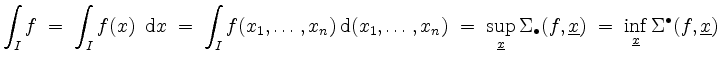
für das Integral von
Anschaulich beziffert das Integral also das Volumen zwischen der
![]() -Ebene und dem Funktionsgraphen,
wobei die Teile unterhalb der
-Ebene und dem Funktionsgraphen,
wobei die Teile unterhalb der
![]() -Ebene negativ zu nehmen sind.
-Ebene negativ zu nehmen sind.
Iterierte Integrale und der Satz von Fubini für Quader.
Für fest gewähltes
![]() betrachte die Quader
betrachte die Quader ![]() mit
mit
![$\displaystyle I \; =\; \underbrace{[a_1,b_1] \times \ldots \times [a_m,b_m]}_{=...
...
\underbrace{[a_{m+1},b_{m+1}] \times \ldots \times [a_n,b_n]}_{=:\; I''}\; .
$](/inhalt/vstatisch/vstatisch62/img26.png)
Der Satz von Fubini für Quader besagt nun, daß einerseits
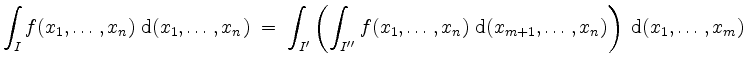
gilt, falls alle auftretenden Integrale existieren, und daß andererseits
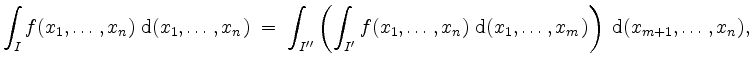
falls wiederum alle auftretenden Integrale existieren. In diesen Fällen läßt sich das Integral von
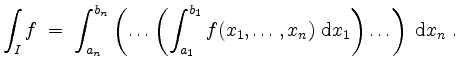
Lebesguesche Nullmengen.
Eine Teilmenge ![]() des
des
![]() heißt Lebesguesche Nullmenge, falls es für alle
heißt Lebesguesche Nullmenge, falls es für alle
![]() eine Folge von
eine Folge von ![]() -dimensionalen Quadern
-dimensionalen Quadern
![]() so gibt, daß
so gibt, daß
Beispiele für Lebesguesche Nullmengen sind etwa
Integration über beschränkte Mengen.
Es seien
![]() beschränkt und
beschränkt und
![]() eine Funktion. Wir definieren die Funktion
eine Funktion. Wir definieren die Funktion
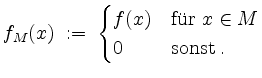
Es sei ![]() ein
ein ![]() -dimensionaler Quader mit
-dimensionaler Quader mit
![]() . Die Funktion
. Die Funktion ![]() heißt (Riemann-) integrierbar
auf
heißt (Riemann-) integrierbar
auf ![]() , falls
, falls ![]() integrierbar auf
integrierbar auf ![]() ist. Dann heißt
ist. Dann heißt
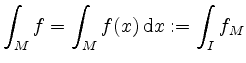
das (Riemann-) Integral von
Meßbare Mengen.
Die Menge ![]() heißt (Jordan-) meßbar, falls die konstante Funktion
heißt (Jordan-) meßbar, falls die konstante Funktion ![]() integrierbar über
integrierbar über ![]() ist,
und dann heißt
ist,
und dann heißt
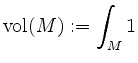
der (Jordan-) Inhalt von
Zum Beispiel ist ein ![]() -dimensionaler Quader meßbar, und sein Jordaninhalt stimmt mit seinem oben eingeführten Volumen überein.
-dimensionaler Quader meßbar, und sein Jordaninhalt stimmt mit seinem oben eingeführten Volumen überein.
Eine meßbare Lebesguesche Nullmenge ![]() hat
hat
![]() .
.
Meßbarkeitskriterium. Eine beschränkte Menge
![]() ist genau dann meßbar, wenn
die Menge der Randpunkte von
ist genau dann meßbar, wenn
die Menge der Randpunkte von ![]() eine Lebesguesche Nullmenge ist.
eine Lebesguesche Nullmenge ist.
Dabei heißt
![]() ein Randpunkt von
ein Randpunkt von ![]() , wenn
, wenn ![]() ein Berührpunkt von
ein Berührpunkt von ![]() , jedoch kein
innerer Punkt von
, jedoch kein
innerer Punkt von ![]() ist. Mit anderen Worten, jede Umgebung von
ist. Mit anderen Worten, jede Umgebung von ![]() enthält sowohl Punkte von
enthält sowohl Punkte von ![]() als auch vom
Komplement von
als auch vom
Komplement von ![]() .
.
Das Lebesguesche Integrabilitätskriterium.
Sei
![]() meßbar. Das Lebesguesche Integrabilitätskriterium besagt, daß eine beschränkte Funktion
meßbar. Das Lebesguesche Integrabilitätskriterium besagt, daß eine beschränkte Funktion
![]() genau dann integrierbar auf
genau dann integrierbar auf ![]() ist, wenn die Menge ihrer
Unstetigkeitspunkte auf
ist, wenn die Menge ihrer
Unstetigkeitspunkte auf ![]() eine Lebesguesche Nullmenge ist.
eine Lebesguesche Nullmenge ist.
Insbesondere sind stetige Funktionen auf meßbaren Mengen integrierbar.
Iterierte Integration, der Satz von Fubini und das Cavalierische Prinzip.
Es sei
![]() beschränkt und
beschränkt und
![]() . Für jedes
. Für jedes
![]() sei
sei
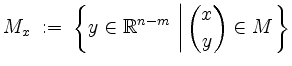
der
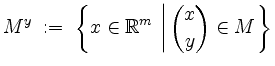
der
Ferner sei
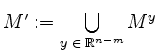 und
und
![]() .
Anschaulich gesprochen ist
.
Anschaulich gesprochen ist ![]() die Projektion von
die Projektion von ![]() auf die
auf die
![]() -Ebene, und
-Ebene, und ![]() die Projektion
von
die Projektion
von ![]() auf die
auf die
![]() -Ebene.
-Ebene.
Der Satz von Fubini besagt nun, daß einerseits
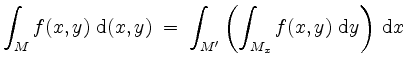
gilt, falls alle auftretenden Integrale existieren, und daß andererseits
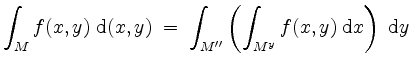
falls wiederum alle auftretenden Integrale existieren. In diesen Fällen läßt sich das Integral von
Insbesondere erhalten wir mit
![]() konstant das Cavalierische Prinzip, welches besagt, daß
konstant das Cavalierische Prinzip, welches besagt, daß
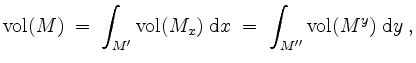
falls alle auftretenden Integrale existieren.
Regeln.
Es seien
![]() ein beschränkte Menge,
ein beschränkte Menge, ![]() integrierbar auf
integrierbar auf ![]() und
und
![]() . Dann gelten folgende Regeln.
. Dann gelten folgende Regeln.
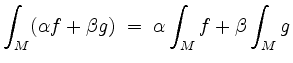 (Linearität).
(Linearität).
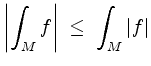 (Dreiecksungleichung).
(Dreiecksungleichung).
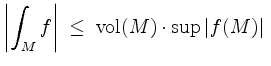 (Prismenungleichung).
(Prismenungleichung).
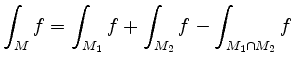 , sofern
, sofern
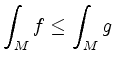 , falls
, falls Der Schwerpunkt und die erste Guldinsche Regel.
Es sei
![]() eine meßbare Menge mit
eine meßbare Menge mit
![]() .
Dann heißt der Punkt
.
Dann heißt der Punkt
![]() mit den
Koordinaten
mit den
Koordinaten
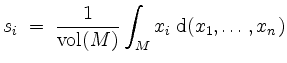
der Schwerpunkt von
Es sei nun
![]() eine meßbare Menge mit Schwerpunkt
eine meßbare Menge mit Schwerpunkt
![]() .
Es sei
.
Es sei ![]() der aus
der aus ![]() entstehende Rotationskörper bei Drehung um die
entstehende Rotationskörper bei Drehung um die
![]() -Achse, definiert durch
-Achse, definiert durch
Nach der ersten Guldinschen Regel ist der Inhalt von
Mit anderen Worten, der Inhalt des Rotationskörpers
| [vorangehende Seite] [nachfolgende Seite] | [Gesamtverzeichnis][Seitenübersicht] |
| automatisch erstellt am 16.2.2011 |