Mo Logo [Home] [Lexikon] [Aufgaben] [Tests] [Kurse] [Begleitmaterial] [Hinweise] [Mitwirkende] [Publikationen]
Mathematik-Online-Kurs: Repetitorium HM II - Mehrdimensionale Analysis

Differenzierbarkeit

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]

Offene Mengen.

Es sei $ n\geq 1$ und $ M \subseteq \mathbb{R}^n$ gegeben. Ein Punkt $ x \in M$ heißt innerer Punkt von $ M$ , falls es ein $ \varepsilon > 0$ gibt, so daß $ B_\varepsilon(x) \subseteq M$ .

Die Menge $ M$ heißt offen, wenn jeder Punkt $ x \in M$ innerer Punkt von $ M$ ist.

Die Menge $ M$ ist genau dann offen, wenn ihr Komplement $ \mathbb{R}^m \setminus M$ abgeschlossen ist.

Partielle Ableitung.

Sei $ M \subseteq \mathbb{R}^n$ . Gegeben seien $ f: M \to \mathbb{R}$ und ein Punkt $ x=(\xi_1, \ldots, \xi_n)^\mathrm{t}\in M$ . Die Funktion $ f$ heißt partiell differenzierbar nach $ x_\nu$ in $ x$ , falls

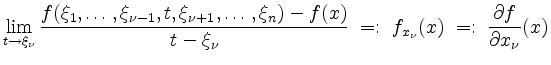
$\displaystyle \lim\limits_{t \to \xi_\nu} \frac{f(\xi_1,\ldots,\xi_{\nu-1},t,\x... ...x)}{t-\xi_\nu} \;=:\; f_{x_\nu}(x) \;=:\; \frac{\partial f}{\partial x_\nu}(x) $

existiert. In diesem Falle heißt der Grenzwert $ f_{x_\nu}(x)$ die partielle Ableitung von $ f$ nach $ x_\nu$ in $ x$ . Mit anderen Worten, ist $ D = \{ t \in \mathbb{R} \vert (\xi_1, \ldots, \xi_{\nu-1},t,\xi_{\nu+1},\ldots,\xi_n) \in M \}$ , so ist in diesem Falle die Funktion

$\displaystyle D \to \mathbb{R}, \; t \mapsto f(\xi_1,\ldots,\xi_{\nu-1},t,\xi_{\nu+1},\ldots,\xi_n) $

differenzierbar in $ t=\xi_\nu$ im Sinne der eindimensionalen Analysis, und ihre Ableitung ist dann gleich $ f_{x_\nu}(x)$ .

Gegeben seien nun $ f: M \to \mathbb{R}^m$ mit den Komponenten $ f=(f_1,\ldots,f_m)^\mathrm{t}$ und ein innerer Punkt $ x \in M$ . Die Funktion $ f$ heißt partiell differenzierbar nach $ x_\nu$ in $ x$ , falls die Funktionen $ f_1, \ldots, f_m$ jeweils partiell differenzierbar nach $ x_\nu$ in $ x$ sind. In diesem Falle heißt der Vektor

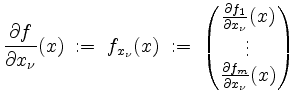
$\displaystyle \frac{\partial f}{\partial x_\nu}(x) \;:=\; f_{x_\nu}(x) \;:=\; ... ...ial x_\nu}(x)\\ \vdots\\ \frac{\partial f_m}{\partial x_\nu}(x) \end{pmatrix}$

die partielle Ableitung von $ f$ nach $ x_\nu$ in $ x$ .

Die Funktion $ f$ heißt partiell differenzierbar in $ x$ , wenn $ f$ partiell differenzierbar nach $ x_\nu$ in $ x$ ist für alle $ \nu\in\{1,\dots,n\}$ . Im Falle $ m = 1$ heißt dann der Vektor

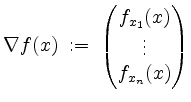
$\displaystyle \nabla f(x) \;:=\; \begin{pmatrix}f_{x_1}(x)\\ \vdots\\ f_{x_n}(x) \end{pmatrix}$

der Gradient von $ f$ in $ x$ .

Die Funktion $ f: M \to \mathbb{R}^m$ heißt partiell differenzierbar, wenn $ f$ partiell differenzierbar in allen Punkten $ x \in M$ ist.

Die Funktion $ f$ heißt stetig partiell differenzierbar, wenn $ f$ partiell differenzierbar ist und die partielle Ableitung $ \frac{\partial f_\mu}{\partial x_\nu}: M \to \mathbb{R}$ stetig ist für alle $ \mu\in\{ 1,\ldots, m\}$ und alle $ \nu\in\{1, \ldots, n\}$ .

Seien nun $ \nu_1,\ldots,\nu_k\in\{1,\ldots,n\}$ gegeben. Dann definiert man rekursiv die $ k$ -fache partielle Ableitung von $ f$ nach $ x_{\nu_1},\ldots,x_{\nu_k}$ in $ x$ durch

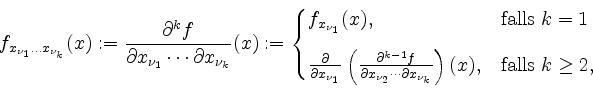
\begin{displaymath} f_{x_{\nu_1}\ldots x_{\nu_k}}(x) := \frac{\partial^k f}{\par... ...al x_{\nu_k}}\right) (x),& \mbox{falls $k\geq 2$,} \end{cases}\end{displaymath}

falls die rechte Seite existiert.

Sei $ k\ge 1$ . Die Funktion $ f: M \to \mathbb{R}^m$ heißt $ k$ -fach stetig differenzierbar, in Zeichen $ f \in C^k(M)$ , falls alle $ k$ -fachen partiellen Ableitungen von $ f$ in allen Punkten $ x \in M$ existieren und stetig sind.

Richtungsableitung.

Sei $ M \subseteq \mathbb{R}^n$ , sei $ f: M \to \mathbb{R}$ eine Funktion, und sei $ x \in M$ ein innerer Punkt. Sei $ v$ eine Richtung im $ \mathbb{R}^n$ , d.h. sei $ v\in\mathbb{R}^n$ und $ \Vert v\Vert=1$ .

Die Funktion $ f$ heißt differenzierbar in Richtung $ v$ in $ x$ , falls

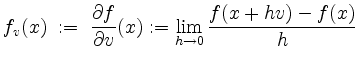
$\displaystyle f_v(x) \;:=\; \frac{\partial f}{\partial v}(x):=\lim_{h\to 0}\frac{f(x+hv)-f(x)}{h} $

existiert. Der Wert $ f_v(x)$ heißt dann die Richtungsableitung von $ f$ in Richtung $ v$ in $ x$ .

Ist speziell $ e_\nu$ der $ \nu$ -te Einheitsvektor in $ \mathbb{R}^n$ , so gilt $ f_{e_\nu}(x) = f_{x_\nu}(x)$ , d.h. die Richtungsableitung in Richtung des $ \nu$ -ten Einheitsvektors ist gleich der partiellen Ableitung nach $ x_\nu$ .

(Totale) Ableitung.

Sei $ M \subseteq \mathbb{R}^n$ , sei $ f: M \to \mathbb{R}^m$ eine Funktion, und sei $ x_0\in M$ ein innerer Punkt.

Die Funktion $ f$ heißt (total) differenzierbar in $ x_0$ , falls es eine Matrix $ A\in\mathbb{R}^{m\times n}$ und eine Funktion $ r:M\to\mathbb{R}^m$ gibt, so daß

$\displaystyle f(x) \; =\; f(x_0) + A(x-x_0) + r(x)\Vert x-x_0\Vert $

für alle $ x \in M$ , und

$\displaystyle \lim_{x\to x_0} r(x)\; =\;0\;. $

Falls $ M \subseteq \mathbb{R}^n$ offen ist, so heißt die Funktion $ f$ (total) differenzierbar, falls sie in jedem Punkt $ x \in M$ differenzierbar ist. (Man setzt ,,total`` manchmal zur Betonung des Unterschiedes zur partiellen Differenzierbarkeit hinzu.)

Ist $ f$ differenzierbar in $ x_0$ , so ist die obengenannte Matrix $ A$ eindeutig bestimmt und heißt die (totale) Ableitung von $ f$ in $ x_0$ , manchmal auch Jacobimatrix von $ f$ in $ x_0$ , und wir schreiben

$\displaystyle f'(x_0) \; := \; A\; . $

Es gilt dann

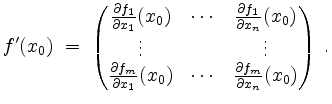
$\displaystyle f'(x_0) \;=\; \begin{pmatrix}\frac{\partial f_1}{\partial x_1}(x_... ...l x_1}(x_0) & \cdots & \frac{\partial f_m}{\partial x_n}(x_0) \end{pmatrix}\;. $

Zum Beispiel ist im Falle $ m = 1$ die Jacobimatrix mit dem Gradienten über die Gleichung $ f'(x_0) = \nabla f(x_0)^\mathrm{t}$ verbunden. (Hier hat man also zwei Begriffe für bis auf Transposition dieselbe Matrix. Dafür gibt es einen Grund, wie wir weiter unten bei den Vektorfeldern sehen werden.)

Ist $ f: M \to \mathbb{R}$ differenzierbar in $ x_0\in M$ , so existieren auch alle Richtungsableitungen von $ f$ in $ x_0$ . Für jede Richtung $ v$ in $ \mathbb{R}^n$ gilt dann

$\displaystyle f_v(x_0) \;=\; f'(x_0) v\;. $

Ist $ f$ differenzierbar in $ x$ , so ist $ f$ insbesondere partiell differenzierbar in $ x$ .

Ist $ M \subseteq \mathbb{R}^n$ offen und $ f: M \to \mathbb{R}^m$ stetig partiell differenzierbar, so ist $ f$ differenzierbar.

Ist $ M \subseteq \mathbb{R}^n$ offen, so gelten folgende Implikationen für eine Funktion $ f: M \to \mathbb{R}^m$ .

\begin{displaymath} \begin{array}{ccccc} \mathrm{stetig partiell differenzierbar... ...enzierbar}\\ &&\Downarrow&&\\ &&\mathrm{stetig}&& \end{array}\end{displaymath}

Regeln für (totale) Ableitungen.

Sei $ M \subseteq \mathbb{R}^n$ , und sei $ x_0\in M$ ein innerer Punkt.

Es seien $ f,\,g\,:\,M \to \mathbb{R}^m$ und $ \gamma: M \to \mathbb{R}$ differenzierbar im inneren Punkt $ x \in M$ , und es seien $ \alpha,\, \beta \,\in\, \mathbb{R}$ . Dann sind auch $ \alpha f + \beta g$ , $ f^\mathrm{t} g$ , $ \gamma f$ in $ x$ differenzierbar, und es gelten die Differentiationsregeln

Sei ferner $ L\subseteq\mathbb{R}^l$ , sei $ g:L \to M$ in einem inneren Punkt $ y \in L$ differenzierbar, und sei $ f:M\longrightarrow\mathbb{R}^m$ differenzierbar im inneren Punkt $ g(y)\in M$ . Wir haben also

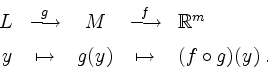
\begin{displaymath} \begin{array}{rcccl} L &\overset{g} {\longrightarrow}& M &\o... ...mm}\\ y &\mapsto & g(y) &\mapsto& (f\circ g)(y)\;. \end{array}\end{displaymath}

Dann ist $ f \circ g$ in $ y$ differenzierbar, und es gilt die Kettenregel

$\displaystyle (f \circ g)'(y) \; =\; f'(g(y)) g'(y) \; . $

Die Hessematrix.

Sei $ M \subseteq \mathbb{R}^n$ offen, und sei $ f: M \to \mathbb{R}$ eine zweifach stetig differenzierbare Funktion.

Die Hessematrix von $ f$ in $ x \in M$ ist durch

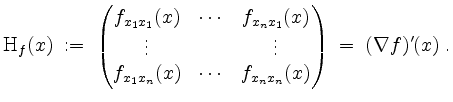
$\displaystyle \mathrm{H}_f(x) \;:=\; \begin{pmatrix}f_{x_1 x_1}(x) & \cdots & f... ...f_{x_1 x_n}(x) & \cdots & f_{x_n x_n}(x) \end{pmatrix}\;=\; (\nabla f)'(x) \;. $

definiert.

Der Satz von Schwarz besagt, daß unter diesen Voraussetzungen $ f_{x_i x_j}=f_{x_j x_i}$ für alle $ i,j \in \{1, \ldots, n\}$ gilt, d.h. daß die Hessematrix $ \mathrm{H}_f(x)$ symmetrisch ist für alle $ x \in M$ .

(Autoren: Künzer/Martin/Tentler/Wahrheit)

Beispiele

Aufgaben

[vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht]
  automatisch erstellt am 16.2.2011